题目内容
【题目】如图所示,一个质量为m,带电量为+q的微粒,从a点以大小为v0的初速度竖直向上射入水平方向的匀强电场中.微粒通过最高点b时的速度大小为2v0方向水平向右.求:
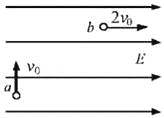
(1)该匀强电场的场强大小E;
(2)a、b两点间的电势差Uab;
(3)该微粒从a点到b点过程中的最小动能EK.
【答案】(1)该匀强电场的场强大小E为![]() ;(2)a、b两点间的电势差
;(2)a、b两点间的电势差![]() 为
为![]() ;(3)该微粒从a点到b点过程中的最小动能
;(3)该微粒从a点到b点过程中的最小动能![]() 为
为![]() 。
。
【解析】试题分析:(1)分析:沿竖直方向和水平方向建立直角坐标系,带电微粒受到重力及电场力作用,两力分别沿竖直方向和水平方向,将物体的运动分解为竖直方向和水平方向的两个分运动:
在竖直方向物体做匀减速运动,加速度ay=g,
在水平方向物体做匀加速运动,初速度为0,加速度ax=![]()
b点是最高点,竖直分速度为0,在竖直方向有:v0="g" t;在水平方向有:2v0=![]()
联立以上两式得:E=![]()
(2)水平位移:x=![]() =v0.t=
=v0.t=![]() ,ab两点间的电势差:Uab=Ex=
,ab两点间的电势差:Uab=Ex=![]()
(3)设重力与电场力的合力为F,其与水平方向的夹角为θ,则:tanθ=![]() =
=![]()
如图所示,开始一段时间内,F与速度方向夹角大于90°,合力做负功,动能减小,后来F与速度夹角小于90°,合力做正功,动能增加,因此,当F与速度v的方向垂直时,小球的动能最小,速度也最小,设为vmin.
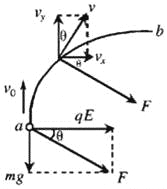
即:tanθ=![]() ,vx=
,vx=![]() =2gt,
=2gt,![]()
联立以上三式得:t=![]() ,vx=
,vx=![]() ,vy=
,vy=![]()
所以最小速度:vmin=![]() =
=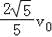 ,所以最小动能
,所以最小动能![]()

练习册系列答案
相关题目