题目内容
5.某种火箭发射前的质量为2.8×106kg,它的第一级产生的推力是3.5×107N,工作时间为150s,喷气速度为2500m/s.试求:(1)每秒消耗的燃料量;
(2)第一级所带的燃料量;
(3)第1s末火箭的速度大小;
(4)第一级火箭燃料耗完时火箭的速度大小.
分析 (1)已知火箭的推力,以及喷气速度,依据冲量定理可求每秒消耗的燃料量.
(2)依据第一问的结果,结合第一级火箭的工作时间可求第一级所带的燃料量.
(3)依据动量守恒可得第1s末火箭的速度大小.
(4)第一级火箭燃料耗完时火箭火箭质量变化,结合动量守恒,可求第一级火箭燃料耗完时火箭的速度大小.
解答 解:(1)设1秒的时间要将m千克的燃料,从速度0变到2500,则:Ft=mv
3.5×107×1=m×2500
解得:m=1.4×104kg.
(2)第一级火箭工作时间为150s,故第一级所带的燃料量为:
M=m×150=1.4×104kg×150=2.1×105kg.
(3)经过1s时间,喷出燃料质量为1.4×104kg.则火箭获得的速度为v′:
M火v′=mv
解得:$v′=\frac{mv}{{M}_{火}}=\frac{1.4×1{0}^{4}×2500}{2.8×1{0}^{6}}=12.5m/s$
(4)第一级火箭燃料耗完时火箭的质量为:
M′=2.8×106-2.1×105=2.59×106kg.
依据动量守恒:M′v′=Mv
解得:$v′=\frac{Mv}{M′}=\frac{2.1×1{0}^{5}×2500}{2.59×1{0}^{6}}$=203m/s.
答:(1)每秒消耗的燃料量为1.4×104kg;
(2)第一级所带的燃料量为2.1×105kg;
(3)第1s末火箭的速度大小为12.5m/s;
(4)第一级火箭燃料耗完时火箭的速度大小为203m/s.
点评 该题的关键是掌握动量守恒,火箭质量在第一秒虽然变化了,但是变化的非常小,故可以忽略不计.

练习册系列答案
相关题目
4.如图甲所示,用一轻质绳拴着一质量为m的小球,在竖直平面内做圆周运动(不计一切阻力),小球运动到最高点时绳对小球的拉力为T,小球在最高点的速度大小为v,其T--v2图象如图乙所示,则( )
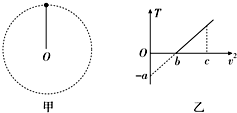

| A. | 轻质绳长为$\frac{am}{b}$ | |
| B. | 当地的重力加速度为$\frac{a}{m}$ | |
| C. | 当v2=c时,轻质绳的拉力大小为$\frac{ac}{b}$+a | |
| D. | 只要v2≥b,小球在最低点和最高点时绳的拉力差均为6a |
17.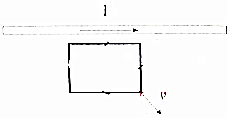 如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )
如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )
 如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )
如图所示.光滑绝缘无限大水平面上固定一通电长直导线.质量为0.02kg的正方形金属框在该水平面内以2m/s、与电流方向成60°角的速度滑出.下列说法中正确的是( )| A. | 金属框中无电流,一直做匀速直线运动 | |
| B. | 金属框最终在水平面上做匀速直线运动 | |
| C. | 金属框最终将静止在水平面上的某处 | |
| D. | 金属框中产生的热量最多为0.04J |
15.下列属于防止静电危害的是( )
| A. | 静电除尘 | B. | 油罐车拖铁路 | C. | 静电喷漆 | D. | 静电复印机 |
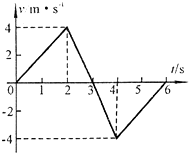 某物体沿一直线运动,其v-t图象如图所示,则第1s内物体运动的加速度大小为2m/s2,方向与速度方向相同(填相同或相反);第3s内物体运动的加速度大小为4m/s2,方向与速度方向相反(填相同或相反);第4s内物体运动的加速度大小为4m/s2,方向与速度方向相同(填相同或相反)前3s内的位移6m,前6s内的位移0m.
某物体沿一直线运动,其v-t图象如图所示,则第1s内物体运动的加速度大小为2m/s2,方向与速度方向相同(填相同或相反);第3s内物体运动的加速度大小为4m/s2,方向与速度方向相反(填相同或相反);第4s内物体运动的加速度大小为4m/s2,方向与速度方向相同(填相同或相反)前3s内的位移6m,前6s内的位移0m.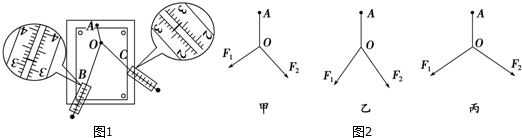
 如图所示,光滑小球静止在两个平面间,一个面恰水平,一个面倾斜,则小球受到的作用力有2个,它们分别是重力和水平面的支持力.
如图所示,光滑小球静止在两个平面间,一个面恰水平,一个面倾斜,则小球受到的作用力有2个,它们分别是重力和水平面的支持力.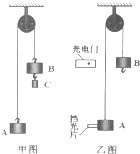 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德(G•Atwood 1746-1807)创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.