��Ŀ����
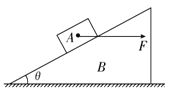
����Ŀ����ͼ��ʾ�������Ĵ��ʹ���ˮƽ��ļнǦ�=30�㣬Ƥ���ڵ綯���Ĵ����£�ʼ�ձ���v0=2m/s���ٶ����У��ֽ�һ����Ϊm=10kg�Ĺ������ɿ�Ϊ�ʵ㣩�������Ƥ���ĵˣ����������͵�h=1.5m�ĸߴ�����֪������Ƥ����Ķ�Ħ�����ئ�= ![]() ��ȡg=10m/s2 �� ����һ�������У���
��ȡg=10m/s2 �� ����һ�������У���
��1�����͵�ʱ�䣻
��2�������봫�ʹ�֮������Ħ�������������ܣ�
��3���綯�����ڴ����������ĵĵ��ܣ�
���𰸡�
��1���⣺�����������Ƥ���ĵˣ��ܵ�������֧����������б�����ϵĻ���Ħ�������ã�������б�����ϣ��������ȼ����˶�����ţ�ٵڶ����ɵã�
��mgcos�ȩ�mgsin��=ma����
�ü��ٶȣ�a=g����cos�ȩ�sin�ȣ�=2.5 m/s2
�蹤������ʱ��t1�ٶ��봫�ʹ���ͬ����t1= ![]() =
= ![]()
�˹����й����ƶ���λ��Ϊ��s1= ![]() =
= ![]() m=0.8m
m=0.8m
�˺��洫�ʹ�һ���������˶���ʱ��Ϊ��t2= ![]() =
= ![]() s=1.1s
s=1.1s
�ʴ��͵�ʱ��Ϊ��t=t1+t2=1.9s
�𣺴��͵�ʱ����1.9s��
��2���⣺��������ڴ��ʹ���λ��Ϊ����s=v0t1��s1=0.8m
����������Ϊ��Q=f��s=��mgcos�ȡ�s=60J
�𣺹����봫�ʹ�֮������Ħ����������������60J��
��3���⣺�綯�����ڴ����������ĵĵ���Ϊ��
E��= ![]() +mgh+Q=230J��
+mgh+Q=230J��
�𣺵綯�����ڴ����������ĵĵ�����230J��
������������һ����Ҫ�����������˶��������ţ�ٵڶ����ɺ��˶�ѧ��ʽ���������λ�ƣ��������Ħ����������������һ����Ҫ�����������ת�����������غ㶨�����綯�������ĵĵ��ܣ�