题目内容
7. 如图所示,半径R=0.40m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的小球,以初速度v0=7.0m/s在水平地面上向左作加速度a=3.0m/s2的匀减速直线运动,求:
如图所示,半径R=0.40m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的小球,以初速度v0=7.0m/s在水平地面上向左作加速度a=3.0m/s2的匀减速直线运动,求:(1)小球若从距A点4.0m的C点出发,落地点离A点多远?
(2)要求小球能进入圆环轨道但不脱轨,小球在地面上的出发点离A点的距离应满足什么条件?(取重力加速度g=10m/s2).
分析 (1)要求AC之间的距离应该首先判定物体能否到达B点,故应该先求出物体到达B点的最小速度,然后根据动能定理求出物体实际到达B点时的速度,由于实际速度大于最小速度,故物体到达B后做平抛运动,最后根据平抛运动的规律求出物体在平抛过程当中水平向的位移.
(2)要使小球通过最高点,则在最高点由重力充当向心力可求得速度;再对全过程由动能定理可求得水平距离.
解答 解:(1)小球向左运动的过程中小球做匀减速直线运动,故有
vA2-v02=-2as
解得vA=$\sqrt{{{v}_{0}}^{2}-2as}$=$\sqrt{49-2×3×4}$=5m/s
如果小球能够到达B点,则在B点的最小速度vmin,
故有mg=$\frac{m{{v}_{min}}^{2}}{R}$
解得vmin=$\sqrt{gR}$=2m/s
而小球从A到B的过程中根据机械能守恒可得
mgh+$\frac{1}{2}m{{v}_{B}}^{2}$=$\frac{1}{2}m{{v}_{A}}^{2}$
解得vB=3m/s
由于VB>vmin
故小球能够到达B点,且从B点作平抛运动,
在竖直方向有
2R=$\frac{1}{2}g{t^2}$
在水平方向有
sAC=vBt
解得:sAC=1.2m
故AC间的距离为1.2m.
(2)要使小球不脱离轨道,则在最高点应有:
mg=m$\frac{{v}^{2}}{r}$
解得:v2=gR=0.4×10=4;
则设水平面上位移为x;
则应有:
-max-2mgR=$\frac{1}{2}$mv2-$\frac{1}{2}$mv02
解得x=4.8m;
则要使物体能通过最高点,小球出发点距A点应小于4.8m;
答:(1)小球若从距A点4.0m的C点出发,落地点离A点1.2m
(2)要求小球能进入圆环轨道但不脱轨,小球在地面上的出发点离A点的距离小于等于4.8m.
点评 解决多过程问题首先要理清物理过程,然后根据物体受力情况确定物体运动过程中所遵循的物理规律进行求解,要注意明确恰好能到达半圆轨道的最高点是一种临界状态.

 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 如图所示,一轻弹簧上端固定在天花板上,现用互成角度的力F1、F2拉弹簧下端至O点,此过程力F1、F2做功分别为3J和4J.现用一个力F拉弹簧下端至O点,该过程力F做功为( )
如图所示,一轻弹簧上端固定在天花板上,现用互成角度的力F1、F2拉弹簧下端至O点,此过程力F1、F2做功分别为3J和4J.现用一个力F拉弹簧下端至O点,该过程力F做功为( )| A. | 3J | B. | 4J | C. | 5J | D. | 7J |
| A. | 物体所受重力与桌面对物体的支持力 | |
| B. | 物体对桌面的压力与桌面对物体的支持力 | |
| C. | 物体反受重力与物体对桌面的压力 | |
| D. | 不存在作用力与反作用力 |
 已知灵敏电流计指针偏转方向与电流方向的关系为:电流从左边接线柱流进电流计,指针向左偏.如果在导电液体的深度h发生变化时观察到指针正向左偏转,则( )
已知灵敏电流计指针偏转方向与电流方向的关系为:电流从左边接线柱流进电流计,指针向左偏.如果在导电液体的深度h发生变化时观察到指针正向左偏转,则( )| A. | 导体芯A所带电荷量在增加,液体的深度h在增大 | |
| B. | 导体芯A所带电荷量在减小,液体的深度h在增大 | |
| C. | 导体芯A所带电荷量在增加,液体的深度h在减小 | |
| D. | 导体芯A所带电荷量在减小,液体的深度h在减小 |
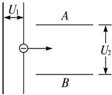 如图所示,电子由静止经加速电场加速后,从AB板的中线垂直射入AB间匀强电场中.若加速电压为U1,偏转电压为U2,其中板长与板间距一定,则( )
如图所示,电子由静止经加速电场加速后,从AB板的中线垂直射入AB间匀强电场中.若加速电压为U1,偏转电压为U2,其中板长与板间距一定,则( )| A. | 电子最终具有的动能Ek=e(U1+U2) | |
| B. | 为使电子能飞出电场,U1必须大于U2 | |
| C. | 电子在两电场间始终做匀变速运动 | |
| D. | 若增大U1,则电子在偏转电场中的运动时间可能不变 |
| A. | 1.5m/s | B. | 2.5m/s | C. | 3.5m/s | D. | 4.5m/s |

