题目内容
如图所示,在第一、二象限存在场强均为E的匀强电场,其中第一象限的匀强电场的方向沿x轴正方向,第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场,矩形区域的AB边与x轴重合。M是第一象限中无限靠近y轴的一点,在M点有一质量为m、电荷量为e的质子,以初速度v0沿y轴负方向开始运动,恰好从N点进入磁场,若 ,不计质子的重力,试求:
,不计质子的重力,试求:
(1)N点横坐标d;
(2)若质子经过磁场最后能无限靠近M点,则矩形区域的最小面积是多少;
(3)在(2)的前提下,该质子由M点出发返回到无限靠近M点所需的时间。
(1)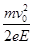 (2)
(2)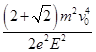 (3)
(3)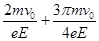
解析试题分析:(1)粒子从M点到N点做类平抛运动,沿x轴正方向做匀加速运动,沿y轴负方向做匀速直线运动,设运动时间为t1,则由平抛运动规律得:
在x轴方向上有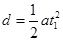 在y轴方向上有:
在y轴方向上有: 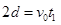
根据牛顿第二定律得: 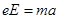
以上各式联立解得: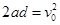 ,
,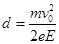
(2)根据运动的对称性作出质子的运动轨迹如图所示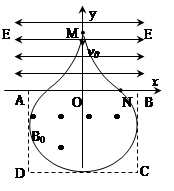
设粒子到达N点时沿x轴正方向分速度为vx,则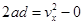 ,即
,即
质子进入磁场时的速度大小为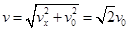
由几何关系知:质子进入磁场时速度方向与x轴正方向夹角为45o
质子在磁场中做圆周运动的半径为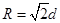
AB边的最小长度为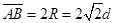
BC边的最小长度为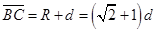
所以矩形区域的最小面积为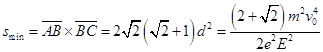
(3)由几何关系知:质子在磁场中运动的圆心角为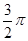 ,运动时间
,运动时间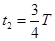
根据线速度的定义知: 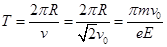
根据对称性,质子在第二象限运动时间与在第一象限运动时间相等,质子在第一象限运动时间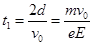
所以该质子由M点出发返回到无限靠近M点所需的时间为: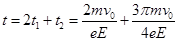
考点:本题考查带电粒子在组合电磁场中的运动问题,意在考查考生综合分析、利用牛顿运动定律和圆周运动知识分析处理带电粒子在电场力和洛仑兹力作用下做不同形式的运动问题的能力。

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目




 =1×108 C/kg、初速度为v0=2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用.
=1×108 C/kg、初速度为v0=2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用. 

