Question

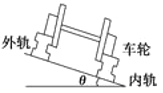
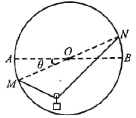
【题目】如图所示，竖直面内有一圆环，圆心为O，水平直径为AB，倾斜直径为MN，AB、MN夹角为θ＝37°，一不可伸长的轻绳长度为L＝R，两端分别固定在圆环的M、N两点，轻质滑轮连接一重力为G的重物，放置在轻绳上，此时轻绳的张力大小为FT，不计滑轮与轻绳的重力，圆环从如图所示位置顺时针缓慢转过2θ角，下列说法正确的是

A.未转动时轻绳的张力大小FT＝GB.未转动时轻绳的张力大小为FT＝G

C.转动过程中轻绳的张力先减小后增大D.转动过程中，轻绳的张力先增大后减小

Answer 1

【答案】BD

【解析】

CD．设绳子总长为L，MN之间的水平距离为s，两绳与竖直方向夹角为，左侧绳长为，右侧绳长为.则由几何关系得：

又：

得到：

设绳子上的张力大小为T，重物的重力为G.以小铁环为研究对象，根据平衡条件得：

2Tcosα=G

因为顺时针转动过程中，M、N间的水平距离先增大后减小，所以轻绳上的张力先增大后减小，故C错误、D正确；

AB．做辅助线MQ//AB交圆于Q，如图：

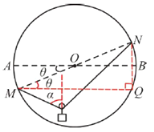
则在中：

，

M、N之间水平距离即：

所以：

解得：

即；而因为有：

解得.故A错误、B正确

故选BD.