题目内容
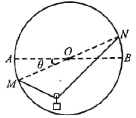
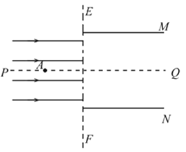
【题目】相距为d的平行金属板M、N，板长也为d，板间可视为匀强电场，两板的左端与虚线EF对齐，EF左侧有水平匀强电场，M、N两板间所加偏转电压为U，PQ是两板间的中轴线。一质量为m、电量大小为q的带电粒子在水平匀强电场中PQ上A点由静止释放，结果恰好从N板的右边緣飞出，A点离EF的距离为
；不计粒子的重力。
(1)求EF左侧匀强电场的电场强度大小；
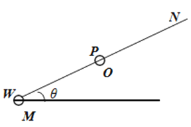
(2)带电粒子从N板的右侧边缘飞出后，只受另一点电荷的库仑力作用，并开始做圆周运动，已知该点电荷固定在PQ上某点，求该点电荷的带电量
.
(3)当带电粒子做圆周运动到M点后，MN板间偏转电压立即变为U，（已知MN板间电场只由偏转电压提供，与点电荷无关）带电粒子最终回到A点，求带电粒子从出发至回到A点所需总时间。
【答案】（1）
（2）
（3）
【解析】
(1)粒子在电场中
上
点由静止释放，做匀加速直线运动，根据动能定理则有：
进入金属板，在偏转电场中，则有：
联立可得：
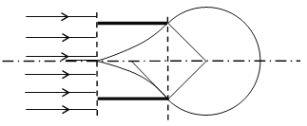
(2)离开N点后带电粒子做圆周运动，有几何关系得圆周运动半径：
库仑力提供向心力，可得：
从点到
点，根据动能定理则有：
由第一问联解上式得：
(3)直线运动阶段，由
可得：
可得：
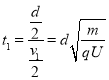
类平抛阶段，则有：
解得：
圆周运动阶段
所需总时间：
总
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
