题目内容
15.某做匀加速直线运动的物体,设它运动全程的平均速度是V1,运动到中间时刻的速度是V2,经过全程一半位置时的速度是V3,则下列关系中正确的是( )| A. | V1=V2>V3 | B. | V1<V2=V3 | C. | V1=V2<V3 | D. | V1>V2=V3 |
分析 匀加速直线运动,前一半时间位移较小,后一半时间位移较大,所以中间时刻的速度比位移中点的速度要小,此外,可以设出初速度、加速度和时间,利用数学方法整理v2,v3的表达式,较好的方法是作v-t图,由图象看两速度的大小关系
解答  解:初速度为v0的匀变速运动的v-t图象如下,由于图线与坐标轴围成的面积可表示为物体运动的位移,
解:初速度为v0的匀变速运动的v-t图象如下,由于图线与坐标轴围成的面积可表示为物体运动的位移,
由图象可得:当时间为$\frac{t}{2}$时,对应的物体速度为v2,此时间内物体运动的位移即图线和坐标轴围成的面积要小于$\frac{S}{2}$;当物体运动位移为$\frac{S}{2}$时,对应的物体速度为v3,有图象明显看出,v2<v3,
根据匀变速运动规律得它运动全程的平均速度等于中间时刻的速度,即v1=v2.
故选:C
点评 选择好的方法可以事半功倍,头脑中要时刻想着图象法解决问题,其优点是形象直观.可以利用图象法推导一下匀加速运动的这两个速度之间的关系是怎样.

练习册系列答案
相关题目
5.如图所示,长为L的细杆AB,从静止开始竖直落下,求它全部通过距下端h处P点所用时间是( )


| A. | $\sqrt{\frac{2h}{g}}$ | B. | $\sqrt{\frac{2(L+h)}{g}}-\sqrt{\frac{2h}{g}}$ | C. | $\sqrt{\frac{2(L+h)}{g}}$ | D. | $\sqrt{\frac{2(L+h)}{g}}-\sqrt{\frac{2L}{g}}$ |
3.物体同时受到同一平面内三个力作用,下列几组力的合力可能为零的是( )
| A. | 1005N,1007N,2014N | B. | 500N,200N,300N | ||
| C. | 100N,500N,1000N | D. | 1000N,1000N,1000N |
20.如果两个力是平衡力,则它们( )
| A. | 一定是作用力和反作用力 | |
| B. | 一定不是作用力和反作用力 | |
| C. | 一定是同种性质的力 | |
| D. | 可能是作用力和反作用力,也可能不是 |
5. 如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,PQ为两个磁场的边界,磁场范围足够大.一边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从左边磁场区域向右运动,当线框运动到分别有一半面积在两个磁场中的位置时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,PQ为两个磁场的边界,磁场范围足够大.一边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从左边磁场区域向右运动,当线框运动到分别有一半面积在两个磁场中的位置时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
 如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,PQ为两个磁场的边界,磁场范围足够大.一边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从左边磁场区域向右运动,当线框运动到分别有一半面积在两个磁场中的位置时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )
如图所示,在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,PQ为两个磁场的边界,磁场范围足够大.一边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从左边磁场区域向右运动,当线框运动到分别有一半面积在两个磁场中的位置时,线框的速度为$\frac{v}{2}$,则下列说法正确的是( )| A. | 位置Ⅱ时线框中的电功率为$\frac{{B}^{2}{a}^{2}{v}^{2}}{4R}$ | |
| B. | 此过程中回路产生的电能为$\frac{3}{8}$mv2 | |
| C. | 位置Ⅱ时线框的加速度为$\frac{{B}^{2}{a}^{2}v}{2mR}$ | |
| D. | 此过程中通过线框截面的电量为$\frac{2B{a}^{2}}{R}$ |
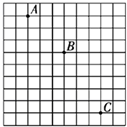 图为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,求
图为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,求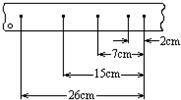 如图所示的纸带是由斜面下滑的小车通过打点计时器拉出来的,打点的时间间隔是0.02s,现按每10个点划分纸带,数据已标在图上,打点计时器打下第二个点是小车的速度为0.175m/s,小车运动的加速度为0.75m/s2.
如图所示的纸带是由斜面下滑的小车通过打点计时器拉出来的,打点的时间间隔是0.02s,现按每10个点划分纸带,数据已标在图上,打点计时器打下第二个点是小车的速度为0.175m/s,小车运动的加速度为0.75m/s2. 如图是电饭煲内部电路工作原理示意图,有两挡开关,使它工作时处于加热状态,休息时处于保温状态(电源电压不变),求
如图是电饭煲内部电路工作原理示意图,有两挡开关,使它工作时处于加热状态,休息时处于保温状态(电源电压不变),求