题目内容
【题目】如图所示，两水平线L1和L2分别是水平向里的匀强磁场的边界，宽度为d，正方形线框abcd由均匀材料制成，其边长为L(L<d)，质量为m，总电阻为R．将线框在磁场上方高h处由静止开始释放，已知线框从开始下落到完全进入磁场过程中通过线框的总电量为q，且ab边刚进入磁场时和刚穿出磁场时的速度相同，求：
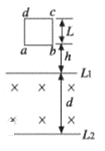
(l)磁场的磁感应强度大小及ab边刚进入磁场时ab两端的电压；
(2)ab边刚进入磁场时线框加速度的大小和方向；
(3)整个线框进入磁场过程所需的时间．
【答案】（1）
；
（2）
方向竖直向上 （3）
【解析】（1）线框在进入磁场的过程中，
①
②
又 q=
△t ③
得：
，所以B=
④
ab边进入磁场前，线框自由下落v02=2gh ⑤
ab边刚进入磁场时切割磁感线产生感应电动势E=BLv0 ⑥
ab两端的电压为U=I
=
⑦
（2）由题中条件可知，ab边进入磁场时和刚穿出磁场时的速度相同，而线框完全进入磁场后做加速度为g的匀加速直线运动，由此可判断ab边刚进入磁场时线框应做减速运动，故加速度方向竖直向上．
由牛顿第二定律可知，BIL-mg=ma ⑧
同时有 I=
⑨
所以 ⑩
（3）设线框全部进入磁场的瞬间速度大小为v1，则：v02-v12=2g（d-L） （12）
线框在进入磁场的过程中，以向上为正方向：BIL-mg=ma
在极短时间△t内，BIL-mg=m
，即 （BIL-mg）△t=m△v
对方程两边求和，∑（BIL-mg）△t=∑m△v，
化简得：BLq-mgt=m（v0-v1） （13）
将各量代入得：
（14）
练习册系列答案
相关题目
