题目内容
1．在水面下同一深处的两个点光源P、Q发出不同颜色的光，在水面上P光照亮的区域大于Q光照亮的区域，下列说法正确的是（ ）| A． | 在真空中P光的传播速度更大 | |
| B． | P光在水中的传播速度小于Q光在水中的传播速度 | |
| C． | 让P光和Q光通过同一双缝干涉装置，P光的条纹间距小于Q光 | |
| D． | P光发生全反射的临界角大于Q光发生全反射的临界角 |
分析 在水面下同一深处的两个点光源P、Q发出不同颜色的光，在水面上P光照亮的区域大于Q光照亮的区域，根据折射定律比较出光的折射率大小，从而比较出光的频率大小、在介质中速度大小关系和波长大小关系．
解答 解：A、光在真空是的传播速度大小是相等的，所以A错误；
B、D、由题，在水面下同一深处的两个点光源P、Q发出不同颜色的光，在水面上P光照亮的区域大于Q光照亮的区域，知P光发生全反射的临界角大，根据sinC=$\frac{1}{n}$，知P光的折射率小．根据v=$\frac{c}{n}$知，P光的折射率小，则P光在水中的传播速度大．故B错误，D正确；
C、因为P光的折射率小，所以P光的频率小，则P光波长一些，故让P光和Q光通过同一双缝干涉装置P光的条纹间距大于Q光，所以C错误．
故选：D
点评 该题考点为光的双缝干涉现象；全反射；解决本题的突破口在于根据光的全反射得出折射率的大小，知道折射率、频率、波长以及在介质中的速度大小关系．
练习册系列答案
相关题目
11．在平直公路上，自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标，它们的位移x（m）随时间t（s）变化的规律为汽车为$x=10t-\frac{1}{4}{t^2}$，自行车为x=6t，则下列说法正确的是（ ）
| A． | 汽车作匀减速直线运动，自行车作匀速直线运动 | |
| B． | 开始经过路标后较小时间内汽车在前，自行车在后 | |
| C． | 当两车速度相等时相距最远 | |
| D． | 当自行车追上汽车时，它们距路标96m |
12．质点的下列运动中，不属于匀变速运动的是（ ）
| A． | 平抛运动 | B． | 竖直上抛运动 | C． | 自由落体运动 | D． | 匀速圆周运动 |
9．下列有关热现象的叙述中正确的是（ ）
| A． | 当分子间的距离增大时，分子力减小，分子势能减小 | |
| B． | 温度越高，分子平均动能越大 | |
| C． | 物体的内能增加，一定要从外界吸收热能 | |
| D． | 一定质量的气体，温度升高时，体积可能不变 |
16．
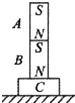如图所示，条形磁铁A、B质量均为m，C为木块，它们放在水平面上静止时，B对A的弹力为F1，C对B的弹力为F2，则F1、F2与重力mg的大小关系正确的是（ ）
如图所示，条形磁铁A、B质量均为m，C为木块，它们放在水平面上静止时，B对A的弹力为F1，C对B的弹力为F2，则F1、F2与重力mg的大小关系正确的是（ ）| A． | Fl=mg，F2=2mg | B． | F1＞mg，F2=2mg | C． | Fl＞mg，F2=mg | D． | F1=mg，F2＞2mg |
6．
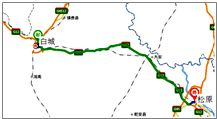松原的查干湖和白城的向海同为国家级自然保护区，近些年旅游事业蓬勃发展，吸引大批海内外游客．设游客甲从白城乘火车去松原，运行184km．游客乙驾车从松原火车站赶往白城火车站行程190km，如图．若二人恰好同时出发且同时到达，则甲乙在两地之间运动的过程中（ ）
松原的查干湖和白城的向海同为国家级自然保护区，近些年旅游事业蓬勃发展，吸引大批海内外游客．设游客甲从白城乘火车去松原，运行184km．游客乙驾车从松原火车站赶往白城火车站行程190km，如图．若二人恰好同时出发且同时到达，则甲乙在两地之间运动的过程中（ ）| A． | 研究甲的行驶路程时可将火车看作质点 | |
| B． | 甲的平均速率小于乙的平均速率 | |
| C． | 甲、乙的平均速度相同 | |
| D． | 题中的“190km”指的是位移 |
13．
如图所示，abcd是由粗细均匀的电阻丝制成的矩形线框水平放置，导体MN有电阻，其电阻大小与ab边电阻大小相同，可在ab边及dc边上无摩擦滑动，且接触良好．匀强磁场（图中未画出）垂直于线框平面，当MN在水平拉力作用下由紧靠ad边向bc边匀速滑动的过程中，以下说法中正确的是（ ）
如图所示，abcd是由粗细均匀的电阻丝制成的矩形线框水平放置，导体MN有电阻，其电阻大小与ab边电阻大小相同，可在ab边及dc边上无摩擦滑动，且接触良好．匀强磁场（图中未画出）垂直于线框平面，当MN在水平拉力作用下由紧靠ad边向bc边匀速滑动的过程中，以下说法中正确的是（ ）| A． | MN中电流先减小后增大 | |
| B． | MN两端电压先减小后增大 | |
| C． | 作用在MN上的拉力先减小后增大 | |
| D． | 矩形线框中消耗的电功率先减小后增大 |
10．下列说法正确的是（ ）
| A． | 机械表是由发条的弹力带动指针走动的 | |
| B． | 用细杆拨动水中的木头，木头受到的弹力是由于木头发生形变而产生的 | |
| C． | 弹簧能恢复形变，铁球挂在弹簧上并静止，弹簧对铁球的弹力等于铁球受到的重力 | |
| D． | 橡皮泥不能恢复形变，铁球放在橡皮泥上并静止，橡皮泥对铁球弹力小于铁球重力 |
14．
如图所示，一根长约为L=20$\sqrt{2}$cm的均匀细杆OB可以绕通过其一端的水平轴在竖直平面内转动，杆最初处于水平位置，杆上距O为a=20cm处放有一小物体（可视为质点），杆与其上小物体最初均处于静止状态．若此杆突然以匀角速度ω绕O顺时针匀速转动．若小物体一定能与杆相碰，则角速度ω的取值范围有（ ）
如图所示，一根长约为L=20$\sqrt{2}$cm的均匀细杆OB可以绕通过其一端的水平轴在竖直平面内转动，杆最初处于水平位置，杆上距O为a=20cm处放有一小物体（可视为质点），杆与其上小物体最初均处于静止状态．若此杆突然以匀角速度ω绕O顺时针匀速转动．若小物体一定能与杆相碰，则角速度ω的取值范围有（ ）| A． | ω＜$\frac{5}{4}$πrad/s | B． | ω＜$\frac{5}{2}$πrad/s | ||
| C． | ω＞$\frac{45}{4}$πrad/s | D． | ω≥$\frac{45}{8}$nπrad/s（n=1，2，3…） |