题目内容
10.已知地球半径为R,地球表面重力加速度为g,地球同步卫星周期为T0.另有一颗轨道在赤道平面内绕地球自西向东运行的卫星,某时刻该卫星能观察到的赤道弧长最大为赤道周长的$\frac{1}{3}$.求:(1)该卫星的周期.
(2)该卫星与地球同步卫星相邻两次经过地球赤道上同一点的正上空所需的时间.
分析 (1)根据万有引力提供向心力列出等式求解.
(2)卫星相邻两次经过地球赤道上某点的上空转过的角度之差为2π,由几何关系列出等式求解.
解答 解:(1)该卫星所观察地球赤道弧长为赤道周长的三分之一,
该圆弧对应的圆心角为120°,由几何关系知该卫星轨道半径为r=2R;
地球表面的物体受到的重力等于万有引力:G$\frac{Mm}{{R}^{2}}$=mg,
卫星做圆周运动,万有引力提供向心力,
由牛顿第二定律得:G$\frac{Mm}{(2R)^{2}}$=m$(\frac{2π}{T})^{2}$•2R,
解得:T=4π$\sqrt{\frac{2R}{g}}$;
(2)设该卫星相邻两次经过地球赤道上某点的上空所需的时间为t,
则:($\frac{2π}{T}$-$\frac{2π}{{T}_{0}}$)t=2π,解得:t=$\frac{4π{T}_{0}\sqrt{\frac{2R}{g}}}{{T}_{0}-4π\sqrt{\frac{2R}{g}}}$;
答:(1)该卫星的周期为4π$\sqrt{\frac{2R}{g}}$.
(2)该卫星与地球同步卫星相邻两次经过地球赤道上同一点的正上空所需的时间为$\frac{4π{T}_{0}\sqrt{\frac{2R}{g}}}{{T}_{0}-4π\sqrt{\frac{2R}{g}}}$.
点评 本题难度中等,明确卫星相邻两次经过地球赤道上某点的上空转过的角度之差为2π,天体运动实际还是圆周运动,只是本类型题物理量较多,公式推导及其复杂.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
20.将四个相同的灯泡分别组成如图所示的甲、乙两种电路并接在相同的端压两端.调节变阻器,使每个灯泡都正常发光.若两个变阻器R1、R2上消耗的功率分别为P1、P2,则P1、P2的大小关系可能为( )


| A. | P2=2P1 | B. | P2=4P1 | C. | P2=8P1 | D. | P2=64P1 |
1.对于一段非纯电阻电路,若加在电路两端的电压为U,通过电路的电流为I,电路中的电阻为R,电路的电功率为P,电路发热的功率为P热,下列关系正确的是( )
| A. | P=IU | B. | I=$\frac{U}{R}$ | C. | P热=I2R | D. | P>P热 |
18. 如图,实线表示某电场的电场线,一带负电的粒子沿虚线所示的路径从a点运动到b点,则( )
如图,实线表示某电场的电场线,一带负电的粒子沿虚线所示的路径从a点运动到b点,则( )
 如图,实线表示某电场的电场线,一带负电的粒子沿虚线所示的路径从a点运动到b点,则( )
如图,实线表示某电场的电场线,一带负电的粒子沿虚线所示的路径从a点运动到b点,则( )| A. | 带电粒子所受电场力变大 | B. | 带电粒子所受电场力变小 | ||
| C. | 带电粒子的电势能变小 | D. | 带电粒子的电势能变大 |
15.一足球运动员开出角球,球的初速度是20m/s,踢出时和水平面的夹角是45°,如果球在飞行过程中,没有被任何一名队员碰到,空气阻力不计,g=10m/s2,球的落地点与开出点之间的距离为( )
| A. | 38.4 m | B. | 40 m | C. | 76.8 m | D. | 153.6 m |
2.滚摆上下摆动,而高度越来越低,说明( )
| A. | 滚摆的机械能守恒 | |
| B. | 能量正在消失 | |
| C. | 只有动能和势能的相互转化 | |
| D. | 减少的机械能转化为内能,但总能量守恒 |
20.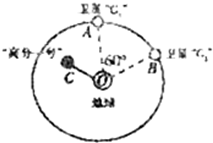 马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置,若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置,若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
 马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置,若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )
马航客机失联后,西安卫星测控中心紧急调动海洋、风云、高分、遥感4个型号近10颗卫星,为地面搜救提供技术支持.特别是“高分一号”突破了空间分辨率、多光谱与大覆盖面积相结合的大量关键技术.如图为“高分一号”与北斗导航系统两颗卫星在空中某一面内运动的示意图.“北斗”系统中两颗卫星“G1”和“G3”的轨道半径均为r,某时刻两颗工作卫星分别位于轨道上的A、B两位置,“高分一号”在C位置,若卫星均顺时针运行,地球表面处的重力加速度为g,地球半径为R,不计卫星间的相互作用力.则以下说法正确的是( )| A. | 卫星“G1”和“G3”的加速度大小相等均为$\frac{{R}^{2}}{r}$g | |
| B. | 卫星“G1”由位置A运动到位置B所需的时间为$\frac{2πr}{3R}$$\sqrt{\frac{r}{g}}$ | |
| C. | 如果调动“高分一号”卫星到达卫星“G3”所在的轨道,必须对其减速 | |
| D. | “高分一号”是低轨道卫星,其所在高度有稀薄气体,运行一段时间后,高度会降低,速度增大,机械能会减小 |

