题目内容
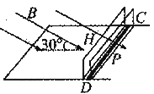
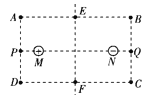
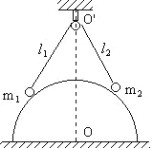
【题目】在热核反应中,磁场换流器可以控制带电粒子的运动轨迹,其简化模型图如图甲所示,通有电流的线圈在其内部形成柱状的匀强磁场,磁场的截面图如图乙所示,磁场半径为R,磁感应强度的大小为B,圆心位于O点。磁场中部有一接地的柱状材料M,其截面圆的圆心也为O点,粒子若打到该材料,将被其吸收。在磁场的边缘A点有一个粒子源,向磁场内部各个方向以某一恒定速率释放质量为m,电荷量为q的负电粒子。建立直角坐标系如图,A点为坐标原点,半径OA与y轴重合。沿+y方向的粒子恰好不与中部柱状材料M接触,直接从磁场外边沿C点射出磁场,C点坐标为(R,R)。不考虑粒子间的相互作用和重力。
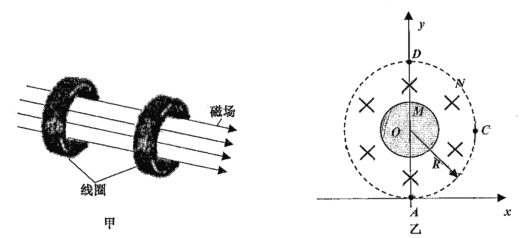
(1)顺这磁场方向看,线圈中的电流方向如何(回答顺时针或逆时针)?求射入磁场的粒子的速度大小和柱状材料M的横截面积;
(2)求粒子穿过x=R直线时对应的y坐标范围;
(3)若在磁场外边缘加装一光滑的特殊环形材料N,粒子与之碰撞时都是完全弹性碰撞的,每次碰撞后粒子的电荷量不变。现使粒子源的速度大小可调,发射方向限制在第一象限方向,某粒子在磁场中运动经![]() 时间恰好与材料N发生第6次碰撞,碰撞点为D(0,2R),求该粒子在A点发射的速度方向和大小。
时间恰好与材料N发生第6次碰撞,碰撞点为D(0,2R),求该粒子在A点发射的速度方向和大小。
【答案】(1)电流方向为顺时针方向,![]() ,
,![]() ; (2)i:[0,R],ii:[
; (2)i:[0,R],ii:[![]() ,2R]; (3)
,2R]; (3)![]() 或
或![]()
【解析】
(1)由安培定则得:电流方向为顺时针方向
由粒子做匀圆周运动有:
![]()
得:
![]()
由几何关系得:柱状材料M的半径![]()
柱状材料M的横截面积为:
![]()
(2)i:粒子初速度方向为第一象限时:穿过x=R直线y坐标范围是[0,R]
ii:当粒子初速度方向为第二象限时:设某粒子轨迹恰好与材料M内切如图:
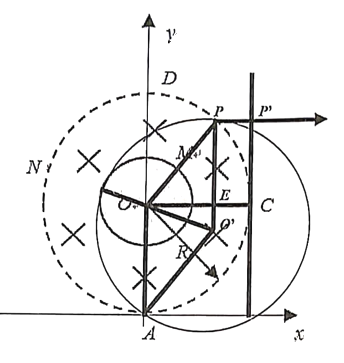
轨迹圆心为![]() 点,由几何关系得:
点,由几何关系得:![]() 为菱形
为菱形
所以粒子在射出点P的速度方向沿+x方向
该+x方向与入射角无关,则所有粒子出磁场时速度均沿+x方向。
设从P点射出的粒子交x=R直线于![]() 点。
点。
由几何关系得:
![]()
![]()
所以:
![]()
![]()
![]() 点的y坐标为
点的y坐标为![]()
穿过x=R直线的y坐标范围是[![]() ,2R]
,2R]
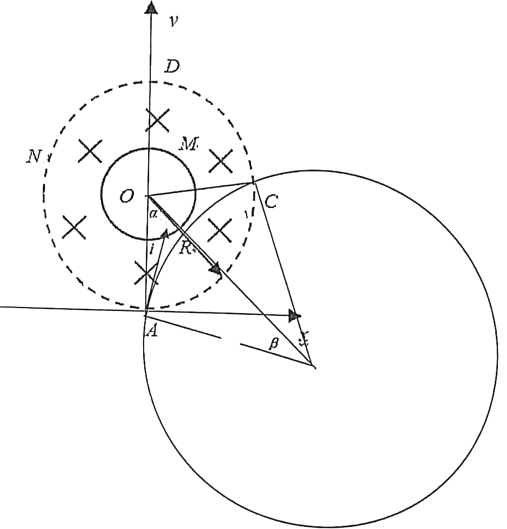
(3)每次碰撞在N边界上转过![]() 弧度,共碰撞6次
弧度,共碰撞6次
所以:
![]()
即:
![]()
每次碰撞轨迹圆心角为![]() ,总时间恰为一个周期
,总时间恰为一个周期![]()
所以:
![]()
即:
![]()
由正弦定理得:
![]()
又:
![]()
设入射时与+y的夹角为i
由几何关系得:
![]()
上述三式得:
![]()
将![]() 代入上式得只能取k=0,1
代入上式得只能取k=0,1
i.k=0时![]() ,粒子发射的方向为与+y夹角为
,粒子发射的方向为与+y夹角为![]()
代入得:
![]()
ii.k=1时![]() ,粒子发射的方向为与+y夹角为
,粒子发射的方向为与+y夹角为![]()
代入得:
![]()

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案