题目内容
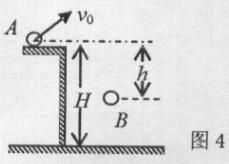
如图所示的半径为R的光滑圆形轨道固定在竖直面内，质量为m的小球A以竖直向下的速度v从与圆心等高处开始沿轨道向下运动，与静止于轨道最低点的B球相撞，碰撞后A、B球恰能分别到达左右两边与圆心等高处。已知地球表面的重力加速度为g。试求：
（1）小球B的质量M＝？
（2）第一次碰撞刚结束时小球A对轨道的压力大小？
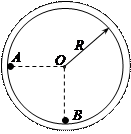
（1）小球B的质量M＝？
（2）第一次碰撞刚结束时小球A对轨道的压力大小？
(1)（1+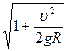
）m (2) 3 mg
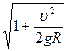）m (2) 3 mg设小球A在与B球相撞前的速度大小为v1，根据机械能守恒
mgR +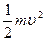
＝
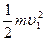············（4分）
得v1＝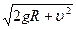
·····（2分）
由于碰撞后A、B球都恰能达到与圆心等高处，所以第一次碰撞刚结束时小球A、B的速度大小相等，方向相反，设速度大小为v2，根据机械能守恒
v2＝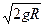
········（4分）
设小球B的质量为M，根据动量守恒
mv1＝Mv2－mv2···········（4分）
解得M＝（1+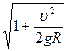）m········（2分）
（2）设第一次碰撞结束时小球A对轨道的压力大小为N，轨道对小球A的支持力为N′，则FN＝FN′···························································（2分）
根据牛顿第二定律FN′－mg＝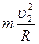
·······（2分）
解得FN＝FN′＝3 mg· ····（2分）
mgR +
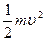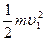＝············（4分）得v1＝
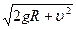·····（2分）由于碰撞后A、B球都恰能达到与圆心等高处，所以第一次碰撞刚结束时小球A、B的速度大小相等，方向相反，设速度大小为v2，根据机械能守恒
v2＝
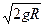········（4分）设小球B的质量为M，根据动量守恒
mv1＝Mv2－mv2···········（4分）
解得M＝（1+
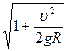）m········（2分）（2）设第一次碰撞结束时小球A对轨道的压力大小为N，轨道对小球A的支持力为N′，则FN＝FN′···························································（2分）
根据牛顿第二定律FN′－mg＝
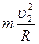·······（2分）解得FN＝FN′＝3 mg· ····（2分）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
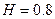
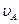和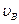
；
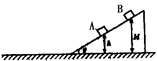
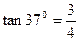，管内无空气阻力，取g=10m/s2）求
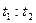
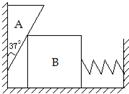
．当棒绕O点向垂直于木块接触边方向转动到棒与水平面间夹角为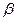
的瞬时，求木块速度的大小．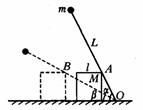
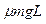
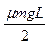
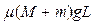
的铁球以某一初速度，在木板的上表面上向左匀速运动，铁球与弹簧刚接触时绳子绷紧，小球的速度仍与初速度相同，弹簧被压缩后，铁球的速度逐渐减小，当速度减小到初速度的一半时，弹簧的弹性势能为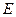
，此时细绳恰好被拉断（不考虑这一过程中的能量损失），此后木板开始向左运动。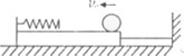
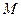，木板开始运动后弹簧的弹性势能最大是多少？
