题目内容
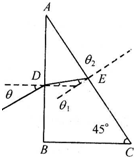
如图所示用某种透明材料制成一块等腰直角棱镜,其顶点为A、B、C,使光线从AB面入射,调整到入射角θ取某个特殊值,恰能使它射入棱镜后在AC面上满足全反射临界条件.试求此材料的折射率n的大小.


依题意画光路图,设光从AB面进入棱镜的入射角为θ时,对应的折射角为θ1,折射光线DE射到AC界面时入射角为θ2,此时光线恰沿AC面射出.
设折射率为n,在△ADE中,(90°-θ1)+(90°-θ2)+45°=180°,得θ1=45°-θ2 sinθ1=sin(45°-θ2)=sin45°cosθ2-cos45°sinθ2=
(cosθ2-sinθ2)
据题意sinθ2=
,则 cosθ2=
=
所以sinθ1=
(
-
)=
(
-1)①
据折射率定义式得n=
②
由①②二式解得:n=
答:此材料的折射率n的大小为
.
设折射率为n,在△ADE中,(90°-θ1)+(90°-θ2)+45°=180°,得θ1=45°-θ2 sinθ1=sin(45°-θ2)=sin45°cosθ2-cos45°sinθ2=
| 1 | ||
|
据题意sinθ2=
| 1 |
| n |
| 1-sin2θ2 |
| ||
| n |
所以sinθ1=
| 1 | ||
|
| ||
| n |
| 1 |
| n |
| 1 | ||
n
|
| n2-1 |
据折射率定义式得n=
| sinθ |
| sinθ1 |
由①②二式解得:n=
(
|
答:此材料的折射率n的大小为
(
|


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目









 和
和 ,则
,则