题目内容
13.在笔直的公路上,一交警驾驶一辆警车停在路边执勤,某时刻该交警发现一辆有违纪行为的货车以大小v=10m/s的速度从他旁边驶过,该交警立即启动警车前去追赶,已知货车从交警旁边(可视为警车和货车在同一位置)驶过到警车开始运动所经历的时间为t0=3s,警车开始运动后以大小a=2m/s2的加速度匀加速行驶,求:($\sqrt{55}$=7.4)(1)警车在追上货车之前距货车的最大距离.
(2)警车追上货车时,警车的速度大小.
分析 (1)在两车速度相等前,货车的速度大于警车,两车的距离越来越大,速度相等之后,货车的速度小于警车,两车的距离越来越小,所以两车速度相等时,距离最大.根据速度相等求出时间,再根据运动学的位移公式求出相距的最大距离.
(2)抓住两车的位移相等,结合位移公式求出追及的时间.
解答 解:(1)设警车运动的时间为t,警车与货车速度相等
$t=\frac{v}{a}=\frac{10}{2}s=5s$
货车位移${x}_{货}^{\;}=v({t}_{0}^{\;}+t)=10×(3+5)=80m$
警车位移:${x}_{警}^{\;}=\frac{1}{2}a{t}_{\;}^{2}=\frac{1}{2}×2×{5}_{\;}^{2}=25m$
最大距离$△x={x}_{货}^{\;}-{x}_{警}^{\;}=80-25=55m$
(2)设经过时间t′警车追上货车,则有
$v({t}_{0}^{\;}+t′)=\frac{1}{2}at{′}_{\;}^{2}$
代入数据:$10×(3+t′)=\frac{1}{2}×2×t{′}_{\;}^{2}$
解得:t′=12.4s
警车速度${v}_{警}^{\;}=at′=2×12.4=24.8m/s$
答:(1)警车在追上货车之前距货车的最大距离为55m.
(2)警车追上货车时,警车的速度大小24.8m/s
点评 解决本题的关键知道速度小者加速追速度大者,两者速度相等时,距离最大.以及知道警车追上货车时,两车的位移相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列说法正确的是( )
| A. | 最早提出用电场线描述电场的物理学家是富兰克林 | |
| B. | 场强处处为零的区域内,电势一定处处相等 | |
| C. | 电势降落的方向一定是场强方向 | |
| D. | 同一电场中等势面分布越密的地方,电势一定越高 |
4.下列说法中正确的是( )
| A. | 重心一定在物体上 | |
| B. | 相互接触的物体间一定有弹力 | |
| C. | 不受到弹力的物体不会受到摩擦力 | |
| D. | 摩擦力的方向一定与物体运动方向相反 |
1.下列关于惯性的说法正确的是( )
| A. | 质量大的物体惯性一定大 | |
| B. | 速度大的物体惯性一定大 | |
| C. | 只有静止或作匀速直线运动的物体才有惯性 | |
| D. | 急速前进的自行车紧急刹车,车上的人向前倾,是由于受自行车向前冲力的作用 |
1.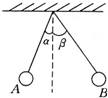 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )| A. | A球的质量较大 | |
| B. | B球的质量较大 | |
| C. | B球受的拉力较大 | |
| D. | 两球接触后,再静止下来,两绝缘细线与竖直方向的夹角变为α′、β′,则有α′=β′ |
5.两相同金属小球A、B所带电荷量分别为+Q、+3Q,固定于相距为2r的两点,此时A、B间库仑力大小为F.若将小球A、B相互接触后,固定于相距为r的另外两点,则此时A、B间库仑力的大小为(两带电球均视为点电荷)( )
| A. | $\frac{1}{3}$F | B. | $\frac{4}{3}$F | C. | $\frac{1}{16}$F | D. | $\frac{16}{3}$F |
6.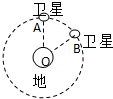 在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
 在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )
在2010年玉树地震的抗震救灾中,我国自主研制的“北斗一号”卫星导航系统发挥了巨大作用,该系统具有导航、定位等功能.“北斗”系统中两颗质量不相等的工作卫星沿同一轨道绕地心O做匀速圆周运动,轨道半径为r.某时刻两卫星分别位于轨道上的A、B两位置,如图所示.若卫星沿顺时针方向运行,地球表面的重力加速度为g,地球半径为R,∠AOB=60°,则以下判断正确的是( )| A. | 质量大的卫星,其加速度也大 | |
| B. | 卫星1向后喷气就一定能追上卫星2 | |
| C. | 卫星1由位置A运动到位置B所需时间为$\frac{πr}{3R}\sqrt{\frac{r}{R}}$ | |
| D. | 卫星1由位置A运动到位置B的过程中万有引力做功为零 |

 如图是一种配有小型风力发电机和光电池的新型路灯,其功率P=120W.该风力发电机的线圈由风叶直接带动,其产生的电流可视为正弦交流电.已知风叶的半径r=1m,风能的利用效率η1=4%,风力发电机的线圈共有N=200匝,磁场的磁感应强度B=0.1T,线圈的面积S1=0.2m2,空气的密度ρ=1.3kg/m3.太阳垂直照射到地面上单位面积上的功率P0=1kW,如果光电池板垂直太阳光方向的平均受光面积为S=1m2,光能的利用效率为η2=20%,π取3,结果均保留2位有效数字.
如图是一种配有小型风力发电机和光电池的新型路灯,其功率P=120W.该风力发电机的线圈由风叶直接带动,其产生的电流可视为正弦交流电.已知风叶的半径r=1m,风能的利用效率η1=4%,风力发电机的线圈共有N=200匝,磁场的磁感应强度B=0.1T,线圈的面积S1=0.2m2,空气的密度ρ=1.3kg/m3.太阳垂直照射到地面上单位面积上的功率P0=1kW,如果光电池板垂直太阳光方向的平均受光面积为S=1m2,光能的利用效率为η2=20%,π取3,结果均保留2位有效数字.