题目内容
【题目】如图所示， 质量相同而电量不同的两个正电荷，从静止开始，经过同一加速电场后，垂直界面进入同一匀强磁场，最后分别打在a、b两点，不计粒子重力，由图可知（ ）
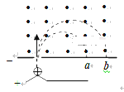
A. 打在a点的粒子速度大
B. 打在b点的粒子速度大
C. a的电荷量大于b的电荷量
D. a、b在磁场中运动的时间相同
【答案】AC
【解析】
根据带电粒子在电场中的加速由动能定理可求得进入磁场时的速度，再对磁场中根据向心力公式可求得半径表达式，从而明确电荷量之间的关系，再代入动能定理表达式即可求得速度大小；根据周期公式和转过的角度进行分析，从而明确时间关系．
A. 经加速电场后，根据动能定理可得：Uq=
mv2 (1)
在磁场中根据牛顿第二定律可得：
(2)
联立解得：R=
，由图可知，a的半径较小，而质量相同，则说明A的电荷较大；则由(1)式可知，打在a点的粒子速度较大，故AC正确，B错误；
D. 由T=
可知，两粒子周期不同，转过的圆心角相同，则可知，时间不同，故D错误。
故选：AC.
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
