题目内容
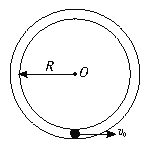
【题目】如图所示，小球m在竖直放置的内壁光滑的圆形细管内做圆周运动，则( )
A. 小球通过最高点的最小速度为v＝
B. 小球通过最高点的最小速度为零
C. 小球通过最高点时一定受到向上的支持力
D. 小球通过最低点时一定受到外管壁的向上的弹力
【答案】BD
【解析】小球在圆形轨道的最高点，由于有支撑，则速度可以为零，故A错误，B正确；小球在圆形轨道的最高点，重力G和弹力N（假设向下）的合力提供向心力，根据牛顿第二定律，有
mg+N=m
；当v=
时，N等于零；当v＜时，N小于零，表明N向上；当v＞时，N大于零，表面N向下；故C错误；小球在圆形轨道的最低点，重力G和弹力N的合力提供向心力，根据牛顿第二定律，有N-mg=m，即N一定向上，即受到外管壁向上的支持力，故D正确；故选BD．
练习册系列答案
相关题目
