题目内容
如图所示,小滑块A的质量m=0.01 kg,与水平地面间的动摩擦因数μ=0.2。用细线悬挂的小球质量均为m=0.01 kg,沿x轴排列,A与第一个小球及相邻两小球间的距离均为s=2.0 m,线长分别为L1、L2、L3、…(图中只画出了三个小球,且小球可视为质点)。开始时,滑块以速度v0=10m/s沿x轴正方向运动,设滑块与小球碰撞后速度互换,且小球均恰好能在竖直平面内做圆周运动。g取10 m/s2。
求:(1)滑块能与几个小球碰撞;
(2)求出碰撞中第n个小球悬线长Ln的表达式;
(3)滑块与第一个小球碰撞后瞬间,悬线对小球拉力FT的大小。
(1)小球在竖直平面内做圆周运动,机械能守恒,返回最低点时速度不变,再次与滑块碰撞互换速度。设滑块滑行总距离为s0,有-μmgs0=0-![]() ,得s0=25 m,n=
,得s0=25 m,n=![]() =12.5,根据题意取12个。
=12.5,根据题意取12个。
(2)滑块与第n个小球碰撞,设小球运动到最高点时速度为v′n 对小球有mg=m![]()
机械能守 ![]() +2mgLn 对滑块有-μmgns=
+2mgLn 对滑块有-μmgns=![]() 联立以上各式解得Ln=
联立以上各式解得Ln=![]() (m)
(m)
(3)滑块做减速运动到第一个小球处与其碰前的速度为v1,则有-μmgs=![]() 滑块与小球相碰撞后互换速度,碰撞后瞬间小球的速度为v1。此时小球受到重力和绳子拉力的作用,根据牛顿第二定律得FT-mg=m
滑块与小球相碰撞后互换速度,碰撞后瞬间小球的速度为v1。此时小球受到重力和绳子拉力的作用,根据牛顿第二定律得FT-mg=m![]() 又因L1=
又因L1=![]() (m) 解得FT=26N
(m) 解得FT=26N

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
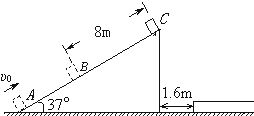 如图所示,小滑块在较长的固定斜面底端,以初速度υ0=8m/s、加速度a=2m/s2沿斜面减速向上滑行,在到达斜面顶端前2s内,滑块所滑过的距离为8m,求:
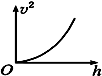
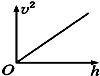
如图所示,小滑块在较长的固定斜面底端,以初速度υ0=8m/s、加速度a=2m/s2沿斜面减速向上滑行,在到达斜面顶端前2s内,滑块所滑过的距离为8m,求: 如图所示,小滑块从一个固定的光滑斜槽轨道顶端无初速开始下滑,用v、t和h分别表示小球沿轨道下滑的速率、时间和距轨道顶端的高度.如图所示的vt图象和v2h图象中可能正确的是( )
如图所示,小滑块从一个固定的光滑斜槽轨道顶端无初速开始下滑,用v、t和h分别表示小球沿轨道下滑的速率、时间和距轨道顶端的高度.如图所示的vt图象和v2h图象中可能正确的是( )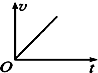
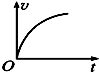
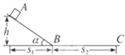 如图所示,小滑块从斜面顶点A由静止滑至水平部分C点而停止.已知斜面高为h,滑块运动的整个水平距离为s,设斜面和水平部分与小滑块的动摩擦因数相同,求此动摩擦因数μ.
如图所示,小滑块从斜面顶点A由静止滑至水平部分C点而停止.已知斜面高为h,滑块运动的整个水平距离为s,设斜面和水平部分与小滑块的动摩擦因数相同,求此动摩擦因数μ.