题目内容
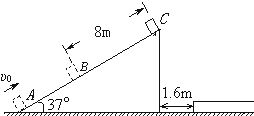 如图所示,小滑块在较长的固定斜面底端,以初速度υ0=8m/s、加速度a=2m/s2沿斜面减速向上滑行,在到达斜面顶端前2s内,滑块所滑过的距离为8m,求:
如图所示,小滑块在较长的固定斜面底端,以初速度υ0=8m/s、加速度a=2m/s2沿斜面减速向上滑行,在到达斜面顶端前2s内,滑块所滑过的距离为8m,求:(1)滑块在斜面上滑行的时间t和斜面的长度L.
(2)若在距离斜面右侧s=1.6m处放置一足够长海绵垫,不计空气阻力,则滑块能否落到垫子上?并说明理由.
(sin37°=0.6,cos37°=0.8,g=10m/s2)
分析:(1)设运动时间为t,小滑块从A到B过程中和从A到C过程中,根据位移时间公式列式联立方程即可求解;
(2)滑块离开斜面顶端做斜抛运动,竖直方向做竖直上抛运动,水平方向做匀速运动,根据运动学基本公式即可求解.
(2)滑块离开斜面顶端做斜抛运动,竖直方向做竖直上抛运动,水平方向做匀速运动,根据运动学基本公式即可求解.
解答:解:(1)小滑块从A到B过程中,有v0(t-2)-
a(t-2)2=x
小滑块从A到C过程中,有v0t-
at2=L
又有L-x=8m
代值计算可得L=15m;t=3s;
(2)能.
理由:滑块离开斜面顶端时的速度为v=v0-at=2m/s,其水平分速度为vx=vcos370=1.6m/s,斜面体高h=Lsin37°=9m,滑块在空中运动的时间t>
>1s,由于惯性,滑块在水平方向匀速运动距离△x=vxt>vx×1s=1.6m,所以能落到垫子上.
解:(1)滑块在斜面上滑行的时间为3s,斜面的长度为15m.(2)滑块能落到垫子上.
| 1 |
| 2 |
小滑块从A到C过程中,有v0t-
| 1 |
| 2 |
又有L-x=8m
代值计算可得L=15m;t=3s;
(2)能.
理由:滑块离开斜面顶端时的速度为v=v0-at=2m/s,其水平分速度为vx=vcos370=1.6m/s,斜面体高h=Lsin37°=9m,滑块在空中运动的时间t>
|
解:(1)滑块在斜面上滑行的时间为3s,斜面的长度为15m.(2)滑块能落到垫子上.
点评:本题主要考查了运动学基本公式的直接应用,要搞清楚滑块的运动情况,抓住位移关系列式求解,难度适中.

练习册系列答案
相关题目
 如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s里,所滑过的距离为
如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s里,所滑过的距离为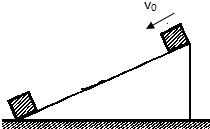 如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s从顶端匀加速向下滑,3s末到达底端,已知斜面的长度L=15m,求:
如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s从顶端匀加速向下滑,3s末到达底端,已知斜面的长度L=15m,求:
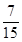 L,其中L为斜面长.求:滑块在斜面上滑行的时间t和斜面的长度L.
L,其中L为斜面长.求:滑块在斜面上滑行的时间t和斜面的长度L.