题目内容
16.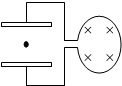 如图所示,线圈内有理想边界的磁场,当磁感应强度均匀增加时,有一带电微粒静止于平行板(两板水平放置)电容器中间.则此微粒带负 电,若线圈匝数为n,平行板电容器间距离为d,微粒质量为m,电量为q,圆形线圈半径为r,则磁感应强度的变化率为$\frac{mgd}{nqπ{r}_{\;}^{2}}$.
如图所示,线圈内有理想边界的磁场,当磁感应强度均匀增加时,有一带电微粒静止于平行板(两板水平放置)电容器中间.则此微粒带负 电,若线圈匝数为n,平行板电容器间距离为d,微粒质量为m,电量为q,圆形线圈半径为r,则磁感应强度的变化率为$\frac{mgd}{nqπ{r}_{\;}^{2}}$.
分析 带电粒子受重力和电场力平衡,由楞次定律可判断极板带电性质,由法拉第电磁感应定律可得出感应电动势解决问题.
解答 解:当磁场均匀增加时,由楞次定律可判断上极板带正电.
所以平行板电容器的板间的电场方向向下,带电粒子受重力和电场力平衡,
所以粒子带负电.
带电粒子受重力和电场力平衡得:mg=F
F=$\frac{U}{d}$q,
而U=n$\frac{△B}{△t}$S
则有,磁感应强度的变化率
$\frac{△B}{△t}=\frac{mgd}{nqπ{r}_{\;}^{2}}$
故答案为:负,$\frac{mgd}{nqπ{r}_{\;}^{2}}$.
点评 本题关键是电容器两端电压的表达,它是联系电磁感应定律和粒子受力情况的桥梁.

练习册系列答案
相关题目
6. 如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板M的边缘以初速度v0射入,沿直线运动并从下极板N的边缘射出,则( )
如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板M的边缘以初速度v0射入,沿直线运动并从下极板N的边缘射出,则( )
 如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板M的边缘以初速度v0射入,沿直线运动并从下极板N的边缘射出,则( )
如图所示,水平放置的平行板电容器两极板间距为d,带负电的微粒质量为m、带电量为q,它从上极板M的边缘以初速度v0射入,沿直线运动并从下极板N的边缘射出,则( )| A. | 微粒一定做匀速直线运动 | B. | 微粒的电势能减少了mgd | ||
| C. | 两极板的电势差为$\frac{mgd}{q}$ | D. | M板的电势低于N板的电势 |
7.某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上.当弹簧自然下垂时,指针指示的刻度数值记作L0,弹簧下端挂一个50g的砝码时,指针指示的刻度数值记作L1;弹簧下端挂两个50g的砝码时,指针指示的刻度数值记作L2;…;挂七个50g的砝码时,指针指示的刻度数值记作L2.
①下表记录的是该同学已测出的6个值,其中有一个数值在记录时有误,它的代表符号是L5
测量记录表:
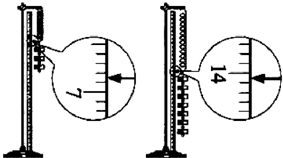
②实验中,L3和L2两个值还没有测定,请你根据上图将这两个测量值填入记录表中.
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L1-Ln=6.90cm,d2=L3-L1=6.90cm,d3=L3-L2=7.00cm.
请你给出第四个差值:d4=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4
表示的式子为:△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{16}$,
代入数据解得△L=1.75cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
①下表记录的是该同学已测出的6个值,其中有一个数值在记录时有误,它的代表符号是L5
测量记录表:
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.10 |

②实验中,L3和L2两个值还没有测定,请你根据上图将这两个测量值填入记录表中.
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L1-Ln=6.90cm,d2=L3-L1=6.90cm,d3=L3-L2=7.00cm.
请你给出第四个差值:d4=L7-L3=7.20cm.
④根据以上差值,可以求出每增加50g砝码的弹簧平均伸长量△L.△L用d1、d2、d3、d4
表示的式子为:△L=$\frac{{d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}}{16}$,
代入数据解得△L=1.75cm.
⑤计算弹簧的劲度系数k=28N/m.(g取9.8m/s2)
1.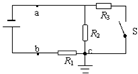 如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )
如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )
 如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )
如图所示电路,R1、R2、R3是定值电阻,c点接地,a、b两接线柱接上直流电源,开关S是断开的,那么,当开关S闭合后( )| A. | ab两点电势均升高 | B. | ab两点电势均降低 | ||
| C. | a点电势升高,b点电势降低 | D. | a点电势降低,b点电势升高 |
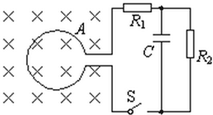 横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:
横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:
 如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直.已知线圈的匝数N=100,边长ab=1.0m、bc=0.5m,电阻r=2Ω,磁感应强度B在0~1s内从零均匀变化到0.2T.在1~5s内从0.2T均匀变化到-0.2T,取垂直纸面向里为磁场的正方向.求:
如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直.已知线圈的匝数N=100,边长ab=1.0m、bc=0.5m,电阻r=2Ω,磁感应强度B在0~1s内从零均匀变化到0.2T.在1~5s内从0.2T均匀变化到-0.2T,取垂直纸面向里为磁场的正方向.求:
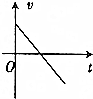
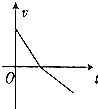
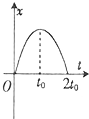
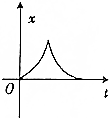
 如图所示,一滑块以初速度v0从固定的粗糙斜面底端上滑,若用x,v,t分别表示滑块的位移、速度和滑行时间,则下列四幅图中能反映滑块从斜面底端出发到返回到斜面底端的是( )
如图所示,一滑块以初速度v0从固定的粗糙斜面底端上滑,若用x,v,t分别表示滑块的位移、速度和滑行时间,则下列四幅图中能反映滑块从斜面底端出发到返回到斜面底端的是( )