题目内容
4.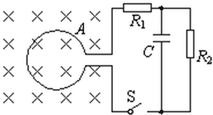 横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:
横截面积S=0.2m2、n=100匝的圆形线圈A处在如图所示的磁场内,磁感应强度变化率为0.02T/s.开始时S未闭合,R1=3Ω,R2=6Ω,C=30 μF,线圈内阻1Ω,求:(1)闭合S后,求回路中的感应电动势的大小;
(2)闭合S后,通过R2的电流的大小和方向;
(3)闭合S后一段时间又断开,问S断开后通过R2的电荷量是多少?
分析 (1)根据法拉第电磁感应定律求出回路中感应电动势的大小;
(2)由闭合电路欧姆定律求回路电流,根据楞次定律求通过${R}_{2}^{\;}$的电流方向;
(3)先求出S闭合后${R}_{2}^{\;}$两端的电压及电容器所带的电量,S断开后通过${R}_{2}^{\;}$的电荷量即S闭合时电容器所带的电荷量
解答 解:(1)磁感应强度变化率的大小为$\frac{△B}{△t}$=0.02 T/s,B逐渐减弱
所以E=n$\frac{S△B}{△t}$=100×0.02×0.2 V=0.4 V
(2)回路电流I=$\frac{E}{{R}_{1}^{\;}+{R}_{2}^{\;}}=\frac{0.4}{4+6}$A=0.04 A,
方向从上向下流过R2
(3)R2两端的电压为U2=$\frac{{R}_{2}^{\;}}{{R}_{1}^{\;}+{R}_{2}^{\;}}E=\frac{6}{4+6}$×0.4 V=0.24 V
所以Q=CU2=30×10-6×0.04 C=7.2×10-6 C
答:(1)闭合S后,回路中的感应电动势的大小为0.4V;
(2)闭合S后,通过R2的电流的大小0.04A和方向从上向下流过${R}_{2}^{\;}$;
(3)闭合S后一段时间又断开,S断开后通过R2的电荷量是$7.2×1{0}_{\;}^{-6}C$
点评 利用法拉第电磁感应定律和闭合电路欧姆定律求解电流大小.S断开后,流过R2的电荷量就是S闭合时C上带有的电荷量

练习册系列答案
相关题目
12.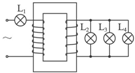 如图所示,一理想变压器的变压比为3:1,图中四只灯泡完全相同.在L1、L2、L3仍然发光的条件下,若没有L4,则( )
如图所示,一理想变压器的变压比为3:1,图中四只灯泡完全相同.在L1、L2、L3仍然发光的条件下,若没有L4,则( )
 如图所示,一理想变压器的变压比为3:1,图中四只灯泡完全相同.在L1、L2、L3仍然发光的条件下,若没有L4,则( )
如图所示,一理想变压器的变压比为3:1,图中四只灯泡完全相同.在L1、L2、L3仍然发光的条件下,若没有L4,则( )| A. | L1、L2、L3变亮 | B. | L1、L2、L3变暗 | ||
| C. | L1变亮,L2、L3变暗 | D. | L1变暗,L2、L3亮度变亮 |
9.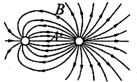 两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )
两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )
 两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )
两点电荷激发的电场所形成的电场线分布如图所示,A、B是电场线上的两点,下列判断正确的是( )| A. | A点的电势高于B点的电势 | |
| B. | 左边点电荷带负电,右边点电荷带正电 | |
| C. | 两点电荷所带电荷量相等 | |
| D. | A点的电场强度大于B点的电场强度 |
 高中电学实验的核心是测电阻,当然所测的对象是不同的,有灯泡的电阻、电阻丝的电阻、电表的电阻、电源的电阻等;所有的方法也不同,有伏安法、半偏法、等效代替法等,其中最常用的是伏安法,测量电路如图所示.
高中电学实验的核心是测电阻,当然所测的对象是不同的,有灯泡的电阻、电阻丝的电阻、电表的电阻、电源的电阻等;所有的方法也不同,有伏安法、半偏法、等效代替法等,其中最常用的是伏安法,测量电路如图所示. 如图所示,某一电场的电场线,其中A点的电势为12V,B点的电势为2V,现把一个q=1×10-6C的正电荷从A点无初速释放,到达B点,则:
如图所示,某一电场的电场线,其中A点的电势为12V,B点的电势为2V,现把一个q=1×10-6C的正电荷从A点无初速释放,到达B点,则: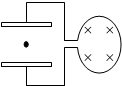 如图所示,线圈内有理想边界的磁场,当磁感应强度均匀增加时,有一带电微粒静止于平行板(两板水平放置)电容器中间.则此微粒带负 电,若线圈匝数为n,平行板电容器间距离为d,微粒质量为m,电量为q,圆形线圈半径为r,则磁感应强度的变化率为$\frac{mgd}{nqπ{r}_{\;}^{2}}$.
如图所示,线圈内有理想边界的磁场,当磁感应强度均匀增加时,有一带电微粒静止于平行板(两板水平放置)电容器中间.则此微粒带负 电,若线圈匝数为n,平行板电容器间距离为d,微粒质量为m,电量为q,圆形线圈半径为r,则磁感应强度的变化率为$\frac{mgd}{nqπ{r}_{\;}^{2}}$.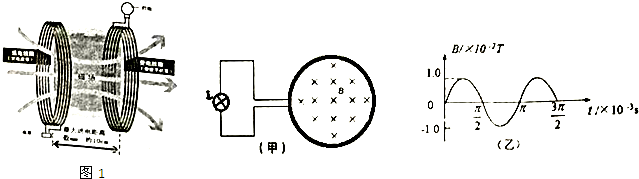
 如图所示,用两根相同的导线绕成匝数分别为n1和n2的圆形闭合线圈A和B,两线圈平面与匀强磁场垂直.当磁感应强度随时间均匀变化时,两线圈中的感应电流之比IA:IB为${n}_{2}^{\;}:{n}_{1}^{\;}$.
如图所示,用两根相同的导线绕成匝数分别为n1和n2的圆形闭合线圈A和B,两线圈平面与匀强磁场垂直.当磁感应强度随时间均匀变化时,两线圈中的感应电流之比IA:IB为${n}_{2}^{\;}:{n}_{1}^{\;}$.