题目内容
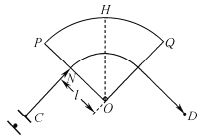
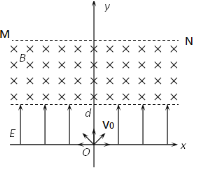
【题目】如图所示，在xOy平面内，位于原点O的放射源向各方向均匀发出速率为v0的带正电粒子，粒子的质量均为m、电荷量均为q。在直线y=d下方分布着一个左右足够宽、方向沿y轴正向的匀强电场E；在直线y=d上方有一平行于x轴的感光板MN，直线y=d和MN之间区域有左右足够宽、方向垂直于纸平面向里的匀强磁场，磁感应强度为B=
。粒子第一次离开电场上边界y=d时，能够到达的最右侧位置为
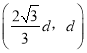，不计粒子重力以及粒子间的相互作用，只考虑每个粒子在电场中和磁场中各运动一次。
（1）求电场强度的大小E；
（2）若要求所有粒子都不能打在感光板MN上，则MN与x轴的最小距离h1是多大？
（3）若要求所有粒子都能打在感光板MN上，则MN与x轴的最大距离h2是多大？当MN与x轴的距离为h2时，MN板上被粒子击中的长度是多少？
【答案】（1）
；（2）3d；（3）2d；
【解析】
（1）沿x轴正方向发射的粒子能够到达最右侧的位置为(
d，d)，由类平抛运动规律得
其中
解得
（2）沿x轴正方向射入的粒子只要打不出磁场，其它粒子一定打不出。
粒子进入磁场的速度为v，根据动能定理可得
解得
v=2v0
根据洛伦兹力提供向心力可得粒子运动轨迹半径为
解得
R=2d
所以MN与x轴的最小距离
h1=R+d=3d
（3）沿-x方向运动的粒子在磁场中只要能够达到荧光屏上，所有粒子都能够打在荧光屏上，如图所示；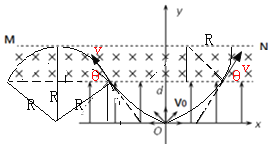
根据（2）可知粒子进入磁场的速度均为v=2v0，运动轨迹半径均为R=2d；
沿-x方向运动的粒子进入磁场时与磁场边界的夹角为θ，则
所以
θ=60°
根据几何关系可得MN到磁场下边缘的距离为y，则
y=R-Rcosθ=d
则MN与x轴的最大距离
h2=d+y=2d；
MN板上被粒子击中左侧到y轴的距离为
MN板上被粒子击中右侧到y轴的距离为
所以MN板上被粒子击中的长度是
