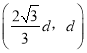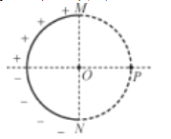
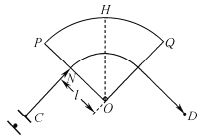
[题目]如图所示为一种质谱仪的工作原理图.圆心角为90°的扇形区域OPQ中存在着磁感应强度大小为B.方向垂直纸面向外的匀强磁场.所有带电粒子经加速电压U加速后从小孔C射出.由磁场边界OP上N点垂直OP进入磁场区域.然后均从边界OQ射出.ON=l.不计粒子重力.(1)若由静止开始加速的某种粒子X从边界OQ射出时速度方向与OQ垂直.其轨迹如图中实线所示.求该粒题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示为一种质谱仪的工作原理图，圆心角为90°的扇形区域OPQ中存在着磁感应强度大小为B、方向垂直纸面向外的匀强磁场，所有带电粒子经加速电压U加速后从小孔C射出，由磁场边界OP上N点垂直OP进入磁场区域，然后均从边界OQ射出，ON=l，不计粒子重力。

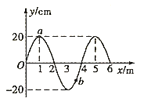
(1)若由静止开始加速的某种粒子X从边界OQ射出时速度方向与OQ垂直，其轨迹如图中实线所示，求该粒子的比荷；

(2)若由静止开始加速的另一种粒子Y，其比荷是X粒子比荷的，求该粒子在磁场区域中运动的时间t。

【答案】(1) ；(2)

【解析】

(1) X粒子在电场中加速的末速度为v0，由动能定理可得

在磁场中由洛伦兹力充当向心力可得

由几何知识可知，粒子的轨道半径为

r=l

联立解得

(2)Y粒子在电场中加速的末速度为v1，由动能定理可得

在磁场中由洛伦兹力充当向心力可得

又

解得

r1=2l

Y粒子在磁场中的轨迹如图所示，圆心为O1，则

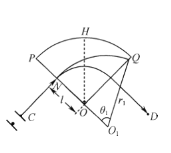
由图可得

由三角函数可知

所以在磁场中运动的时间为

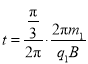
联立解得

练习册系列答案

A. 滑块的加速度大小为5 m/s2

B. 滑块的初速度为5 m/s

C. 滑块运动的总时间为3 s

D. 滑块运动的总位移为4.5 m

【题目】如图所示，足够长的传送带与水平面的夹角为θ，传送带以速度v0逆时针匀速转动。在传送带的上端轻轻放置一个质量为m的小木块，小木块与传送带间的动摩擦因数μ>tanθ，则能客观地反映小木块的速度随时间变化关系的图象是（）

A.B.C.D.

【题目】如图所示,质量的木块A套在水平杆上,并用轻绳将木块与质量的小球B相连.今用跟水平方向成角的力,拉着球带动木块一起向右匀速运动,运动中M、m相对位置保持不变,取.求:

(1)运动过程中轻绳与水平方向夹角;

(2)木块与水平杆间的动摩擦因数为.

(3)当为多大时,使球和木块一起向右匀速运动的拉力最小?

【题目】如图所示，MN 是一半圆形绝缘线，O 点为圆心，P 为绝缘线所在圆上一点，且 OP垂直于 MN，等量异种电荷分别均匀分布在绝缘线上、下圆弧上．下列说法中正确的( )

A.O 点处和 P 点处的电场强度大小相等，方向相同

B.O 点处和 P 点处的电场强度大小不相等，方向相同

C.将一正点电荷沿直线从 O 移动到 P，电场力始终不做功

D.将一正点电荷沿直线从 O 移动到 P，电势能增加

【题目】在《探究感应电流方向的规律》实验中

（1）用试触的方法确定电流方向与电流计指针偏转方向的关系。如图(1)所示实验表明，如果电流从负接线柱流入指针将向______偏转（填左或右）。

（2）观察如图（2）所示的线圈绕线方向，若电流从A流入到B流出，从上向下看电流的方向为______（填顺时针或逆时针）。

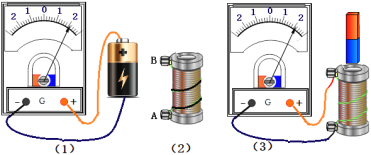
（3）用如图（3）所示的实验装置，若电流表指针向右偏转，则线圈中感应电流产生的磁场的方向_______（填向上或向下）。用电流表观察感应电流的方向，然后判断感应电流的磁场方向，得到如下实验记录。

磁铁的磁场方向	向下	向下	向上	向上
磁铁的磁通量的变化	增大	减小	增大	减小
感应电流的磁场方向	向上	向下	向下	向上

由些得出下列判断中正确的是_________

A．感应电流的磁场方向和磁铁的磁场方向一定相反

B．感应电流的磁场方向和磁铁的磁场方向一定相同

C．磁通量增大时，感应电流的磁场方向和磁铁的磁场方向一定相反

D．磁通量减小时，感应电流的磁场方向和磁铁的磁场方向一定相反

【题目】如图所示，在xOy平面内，位于原点O的放射源向各方向均匀发出速率为v0的带正电粒子，粒子的质量均为m、电荷量均为q。在直线y=d下方分布着一个左右足够宽、方向沿y轴正向的匀强电场E；在直线y=d上方有一平行于x轴的感光板MN，直线y=d和MN之间区域有左右足够宽、方向垂直于纸平面向里的匀强磁场，磁感应强度为B=。粒子第一次离开电场上边界y=d时，能够到达的最右侧位置为，不计粒子重力以及粒子间的相互作用，只考虑每个粒子在电场中和磁场中各运动一次。