题目内容
7.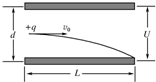 如图所示,带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内,恰好沿下板的边缘飞出.已知板长为L,板间距离为d,板间电压为U,带电粒子的电荷量为q,粒子通过平行金属板的时间为t(不计粒子的重力),则( )
如图所示,带正电的粒子以一定的初速度v0沿两板的中线进入水平放置的平行金属板内,恰好沿下板的边缘飞出.已知板长为L,板间距离为d,板间电压为U,带电粒子的电荷量为q,粒子通过平行金属板的时间为t(不计粒子的重力),则( )| A. | 在前$\frac{t}{2}$时间内,电场力对粒子做的功为$\frac{3Uq}{8}$ | |
| B. | 在后$\frac{t}{2}$时间内,电场力对粒子做的功为$\frac{Uq}{4}$ | |
| C. | 粒子的出射速度偏转角满足tan θ=$\frac{d}{L}$ | |
| D. | 粒子前$\frac{d}{4}$和后$\frac{d}{4}$的过程中,电场力冲量之比为$\sqrt{2}$:1 |
分析 带正电的粒子进入水平放置的平行金属板内,做类平抛运动,竖直方向做初速度为0的匀加速运动,由推论可求出在前$\frac{t}{2}$时间内和在后$\frac{t}{2}$时间内竖直位移之比,由动能定理求出电场力做功.将出射的速度进行分解,求出出射速度偏转角正切.由冲量的定义I=Ft求电场力冲量之比.
解答 解:A、B设粒子在前$\frac{t}{2}$时间内和在后$\frac{t}{2}$时间内竖直位移分别为y1、y2,则y1:y2=1:3,得y1=$\frac{1}{8}$d,y2=$\frac{3}{8}d$,则在前$\frac{t}{2}$时间内,电场力对粒子做的功为W1=q•$\frac{1}{8}U$=$\frac{1}{8}qU$,在后$\frac{t}{2}$时间内,电场力对粒子做的功为W2=q$•\frac{3}{8}U$=$\frac{3}{8}qU$.故A正确,B错误.
C、粒子的出射速度偏转角正切为tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{at}{{v}_{0}}$=$\frac{\frac{1}{2}a{t}^{2}}{\frac{1}{2}{v}_{0}t}$=$\frac{\frac{1}{2}d}{\frac{1}{2}L}$=$\frac{d}{L}$.故C正确.
D、根据推论可知,粒子前$\frac{d}{4}$和后$\frac{d}{4}$的过程中,运动时间之比为1:($\sqrt{2}$-1),电场力是恒力,由冲量公式I=Ft,则得电场力冲量之比为1:($\sqrt{2}-1$)=($\sqrt{2}$+1):1.故D错误.
故选:AC
点评 本题是类平抛运动,要熟练掌握其研究方法:运动的合成与分解,并要抓住竖直方向初速度为零的匀加速运动的一些推论,研究位移和时间关系.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案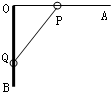 如图所示,直角支架的水平杆OA粗糙,竖直杆OB光滑,两个质量相同的小球P和Q分别套在OA和OB上,P和Q用不可伸长的轻绳连接,处于静止状态.若将小球P稍微向左移动少许后,P、Q仍静止.设杆对P的弹力为N,摩擦力为f,绳的张力为F,则与移动前相比较,下列说法正确的是( )
如图所示,直角支架的水平杆OA粗糙,竖直杆OB光滑,两个质量相同的小球P和Q分别套在OA和OB上,P和Q用不可伸长的轻绳连接,处于静止状态.若将小球P稍微向左移动少许后,P、Q仍静止.设杆对P的弹力为N,摩擦力为f,绳的张力为F,则与移动前相比较,下列说法正确的是( )| A. | N不变 | B. | f增大 | C. | Q的合力增大 | D. | F减小 |
| A. | 摩擦力的方向总与物体的运动方向相反 | |
| B. | 摩擦力的大小与相应的正压力成正比 | |
| C. | 运动着的物体不可能受静摩擦力作用,只能受滑动摩擦力作用 | |
| D. | 摩擦力可以充当动力,也可以充当阻力 |
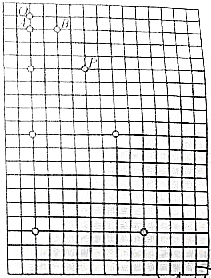 在精细研究平抛运动规律中,如图是一幅平抛物体与自由落体对比的频闪照片,A、B两球初时刻均在O点,A球从O点做自由落体运动的同时,B球以一定的初速度水平抛出,已知图中正方形小方格边长为l,重力加速度为g,P点为B球运动过程中的一个点,根据频闪照片( )
在精细研究平抛运动规律中,如图是一幅平抛物体与自由落体对比的频闪照片,A、B两球初时刻均在O点,A球从O点做自由落体运动的同时,B球以一定的初速度水平抛出,已知图中正方形小方格边长为l,重力加速度为g,P点为B球运动过程中的一个点,根据频闪照片( )| A. | 可判定平抛运动水平方向是匀速运动,竖直方向是自由落体运动 | |
| B. | 可求出相机闪光频率为$\sqrt{\frac{g}{l}}$ | |
| C. | 可以判断B球竖直方向的运动不影响水平方向的运动 | |
| D. | 可以求出B球经过P点的速度大小为$\sqrt{2gl}$ |
 如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为mA=10kg,mB=20kg,A、B之间、B与地面之间的动摩擦因数均为μ=0.5.一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为37°,今欲用水平拉力F将物体B匀速向右拉出,(取g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为mA=10kg,mB=20kg,A、B之间、B与地面之间的动摩擦因数均为μ=0.5.一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为37°,今欲用水平拉力F将物体B匀速向右拉出,(取g=10m/s2,sin37°=0.6,cos37°=0.8)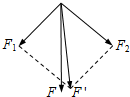 如图所示,是某同学在“验证力的平行四边形定则”的实验中,根据实验数据按照一定的标度画出的力的图示.F1、F2、F、F′中不是由弹簧测力计测得的力是F′(填字母).
如图所示,是某同学在“验证力的平行四边形定则”的实验中,根据实验数据按照一定的标度画出的力的图示.F1、F2、F、F′中不是由弹簧测力计测得的力是F′(填字母).


