题目内容
9.一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,动能减小为原来的$\frac{1}{4}$,不考虑卫星质量的变化,则变轨前后卫星的( )| A. | 向心加速度大小之比为16:1 | B. | 角速度大小之比为2:1 | ||
| C. | 周期之比为1:8 | D. | 轨道半径之比为1:4 |
分析 根据万有引力提供向心力,通过线速度的变化得出轨道半径的变化,从而得出向心加速度、周期、角速度的变化.
解答 解:A、由万有引力提供向心力,
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=mω2r=ma
v=$\sqrt{\frac{GM}{r}}$,
根据动能减小为原来的$\frac{1}{4}$可知,速度减小为原来的$\frac{1}{2}$,轨道半径增加到原来的4倍,即轨道半径之比为1:4,
a=$\frac{GM}{{r}^{2}}$,所以向心加速度大小之比为16:1,故A正确,D正确;
B、ω=$\sqrt{\frac{GM}{{r}^{3}}}$,轨道半径之比为1:4,可知角速度减小为原来的$\frac{1}{8}$,角速度大小之比为8:1,故B错误;
C、T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,轨道半径之比为1:4,所以周期之比为1:8,故C正确;
故选:ACD.
点评 解决本题的关键掌握万有引力提供向心力,知道线速度、角速度、周期、向心加速度与轨道半径的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.在圆轨道上运行的质量为m的人造地球卫星,到地面距离等于地球半径,地面处的重力加速度为g,则( )
| A. | 卫星的线速度为$\sqrt{2Rg}$ | B. | 卫星的周期为$4π\sqrt{\frac{2R}{g}}$ | ||
| C. | 卫星的加速度为$\frac{g}{2}$ | D. | 卫星运行的角速度为$\frac{1}{4}\sqrt{\frac{2g}{R}}$ |
4.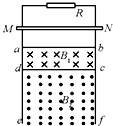 如图所示,足够长的光滑“П”型金属导体框竖直放置,除电阻R外其余部分阻值不计.质量为m的金属棒MN与框架接触良好.磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,当金属棒进入磁场B1区域后,恰好做匀速运动.以下说法中正确的有( )
如图所示,足够长的光滑“П”型金属导体框竖直放置,除电阻R外其余部分阻值不计.质量为m的金属棒MN与框架接触良好.磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,当金属棒进入磁场B1区域后,恰好做匀速运动.以下说法中正确的有( )
 如图所示,足够长的光滑“П”型金属导体框竖直放置,除电阻R外其余部分阻值不计.质量为m的金属棒MN与框架接触良好.磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,当金属棒进入磁场B1区域后,恰好做匀速运动.以下说法中正确的有( )
如图所示,足够长的光滑“П”型金属导体框竖直放置,除电阻R外其余部分阻值不计.质量为m的金属棒MN与框架接触良好.磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,当金属棒进入磁场B1区域后,恰好做匀速运动.以下说法中正确的有( )| A. | 若B2=B1,金属棒进入B2区域后仍保持匀速下滑 | |
| B. | 若B2=B1,金属棒进入B2区域后将加速下滑 | |
| C. | 若B2<B1,金属棒进入B2区域后先加速后匀速下滑 | |
| D. | 若B2>B1,金属棒进入B2区域后先减速后匀速下滑 |
14.用跨过定滑轮的绳把湖中小船拉靠岸,如图所示,已知拉绳的速度v不变,则船速( )


| A. | $\frac{v}{sinθ}$ | B. | $\frac{v}{cosθ}$ | C. | vcosθ | D. | vsinθ |
1.下列物体中,机械能守恒的是(空气阻力均不计)( )
| A. | 正在升空的热气球 | B. | 被匀速向上吊起的集装箱 | ||
| C. | 光滑曲面上自由运动的物体 | D. | 斜抛出去在空中运动的铅球 |
 海军进行登陆演练,如图所示,假设一艘战舰因吨位巨大,只能停锚在离海岸登陆点s=1.1km处.登陆队员需要从较高的军舰甲板上,利用绳索下滑到登陆快艇上再进行登陆接近目标,若绳索两端固定好后,绳索可以近似看成与竖直方向的夹角θ=37°的斜面.队员甲由静止开始匀加速滑到某最大速度,再以大小相等的加速度匀减速滑至快艇,速度刚好为零.已知军舰甲板到快艇的竖直高度H=20m,在队员甲开始下滑时,队员乙在甲板上同时开始向快艇平抛救生圈,第一个救生圈刚落到快艇,紧接着以相同的初速度抛第二个,第二个救生圈刚好与甲队员同时抵达快艇.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.(人、救生圈和快艇均可视为质点,忽略空气阻力).问:
海军进行登陆演练,如图所示,假设一艘战舰因吨位巨大,只能停锚在离海岸登陆点s=1.1km处.登陆队员需要从较高的军舰甲板上,利用绳索下滑到登陆快艇上再进行登陆接近目标,若绳索两端固定好后,绳索可以近似看成与竖直方向的夹角θ=37°的斜面.队员甲由静止开始匀加速滑到某最大速度,再以大小相等的加速度匀减速滑至快艇,速度刚好为零.已知军舰甲板到快艇的竖直高度H=20m,在队员甲开始下滑时,队员乙在甲板上同时开始向快艇平抛救生圈,第一个救生圈刚落到快艇,紧接着以相同的初速度抛第二个,第二个救生圈刚好与甲队员同时抵达快艇.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.(人、救生圈和快艇均可视为质点,忽略空气阻力).问: 如图所示,一质量为M的塑料球容器放在桌面上,它的内部有劲度系数为k的轻弹簧直立固定与容器的内壁底部,弹簧上端轻绝缘系住一只带正电荷量为q,质量为m的小球,从加上一个向上的匀强电场,场强缓慢增强为E的时候,容器对桌面压力恰好为零,问:
如图所示,一质量为M的塑料球容器放在桌面上,它的内部有劲度系数为k的轻弹簧直立固定与容器的内壁底部,弹簧上端轻绝缘系住一只带正电荷量为q,质量为m的小球,从加上一个向上的匀强电场,场强缓慢增强为E的时候,容器对桌面压力恰好为零,问: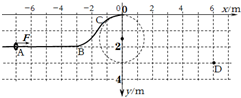 在竖直平面内固定一轨道ABCO,AB段水平放置,长为4m,BCO段弯曲且光滑;一质量为1.0kg、可视作质点的圆环套在轨道上,圆环与轨道AB段之间的动摩擦因数为0.5.建立如图所示的直角坐标系,圆环在沿x轴正方向的恒力F作用下,从A(-7,2)点由静止开始运动,到达原点O时撤去恒力F,圆环从O(0,0)点水平飞出后经过D(6,3)点.重力加速度g取10m/s2,不计空气阻力.求:(答案可用根式表示)
在竖直平面内固定一轨道ABCO,AB段水平放置,长为4m,BCO段弯曲且光滑;一质量为1.0kg、可视作质点的圆环套在轨道上,圆环与轨道AB段之间的动摩擦因数为0.5.建立如图所示的直角坐标系,圆环在沿x轴正方向的恒力F作用下,从A(-7,2)点由静止开始运动,到达原点O时撤去恒力F,圆环从O(0,0)点水平飞出后经过D(6,3)点.重力加速度g取10m/s2,不计空气阻力.求:(答案可用根式表示)