题目内容
 如图所示,有一半径为R的半圆形圆柱面MPQ,质量为2m的A球与质量为m的B球,用轻质绳连接后挂在圆柱面边缘.现将A球从边缘M点由静止释放,若不计一切摩擦,
如图所示,有一半径为R的半圆形圆柱面MPQ,质量为2m的A球与质量为m的B球,用轻质绳连接后挂在圆柱面边缘.现将A球从边缘M点由静止释放,若不计一切摩擦,求(1)A球沿圆柱面滑到最低点P时的速度大小.
(2)A球沿圆柱面滑到最低点P的过程中绳子对A,对B,对AB所组成的系统各做多少功.
分析:(1)先根据几个关系求出A球和B球速度的关系和位移的大小,再对AB整体运用动能定理即可求解;
(2)先对A运用动能定理即可求出绳对A做的功,对AB组成的系统,绳子的力为内力,故绳子对系统做的功为0,绳对B做的功等于负的绳子对A所做的功.
(2)先对A运用动能定理即可求出绳对A做的功,对AB组成的系统,绳子的力为内力,故绳子对系统做的功为0,绳对B做的功等于负的绳子对A所做的功.
解答:解:当A球运动到P点时,作出图象如图所示:
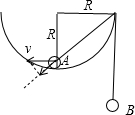
设A球的速度为v,根据几何关系可知B球的速度为
v,B球上升的高度为
R
对AB小球整体运用动能定理得:
?2mv2+
m(
v)2=2mgR-mg
R
解得:v=
gR
对A运用动能定理的:
2mgR+WA=
?2mv2
解得:WA=-
mgR-
mgR
对AB组成的系统,绳子的力为内力,故绳子对系统做的功为0,
所以WB=-WA=
mgR+
mgR
答:(1)A球沿圆柱面滑到最低点P时的速度大小为
gR.
(2)A球沿圆柱面滑到最低点P的过程中绳子对A做功为-
mgR-
mgR,对B做功为
mgR+
mgR,对AB所组成的系统做功为0.

设A球的速度为v,根据几何关系可知B球的速度为
| ||
| 2 |
| 2 |
对AB小球整体运用动能定理得:
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
解得:v=
|
对A运用动能定理的:
2mgR+WA=
| 1 |
| 2 |
解得:WA=-
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
对AB组成的系统,绳子的力为内力,故绳子对系统做的功为0,
所以WB=-WA=
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
答:(1)A球沿圆柱面滑到最低点P时的速度大小为
|
(2)A球沿圆柱面滑到最低点P的过程中绳子对A做功为-
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
点评:本题主要考查了动能定理得直接运用,做题时结合几何关系求解,注意AB球的速度不等.

练习册系列答案
相关题目
 如图所示,有一半径为R质量为m的半球形凹槽P,放在光滑的水平地面上,一面紧靠在光滑的墙壁上,在槽口正上方某处有一质量为m的小球,由静止释放,落下后可沿光滑的球面滑下.试问:
如图所示,有一半径为R质量为m的半球形凹槽P,放在光滑的水平地面上,一面紧靠在光滑的墙壁上,在槽口正上方某处有一质量为m的小球,由静止释放,落下后可沿光滑的球面滑下.试问: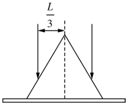 (2012?湖南模拟)桌面上有一玻璃圆锥,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图所示,有一半径为
(2012?湖南模拟)桌面上有一玻璃圆锥,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图所示,有一半径为 如图所示,有一半径为r的导电圆环处于磁感应强度为B的匀强磁场中,磁场方向垂直纸面向里且与圆环平面垂直,圆环的电阻为R.若磁感应强度B在时间△t内均匀减小至零,则此过程( )
如图所示,有一半径为r的导电圆环处于磁感应强度为B的匀强磁场中,磁场方向垂直纸面向里且与圆环平面垂直,圆环的电阻为R.若磁感应强度B在时间△t内均匀减小至零,则此过程( )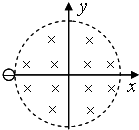 如图所示,有一半径为R、有明显边界的圆形匀强磁场区域,磁感应强度为B.今有一电子沿x轴正方向射入磁场,恰好沿y轴负方向射出.如果电子的荷质比为
如图所示,有一半径为R、有明显边界的圆形匀强磁场区域,磁感应强度为B.今有一电子沿x轴正方向射入磁场,恰好沿y轴负方向射出.如果电子的荷质比为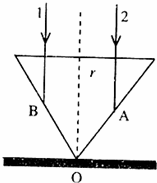 在桌面上有一个倒立的透明的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.r为已知,求:
在桌面上有一个倒立的透明的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.r为已知,求: