题目内容
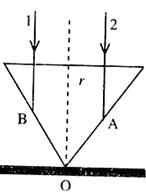
 在桌面上有一个倒立的透明的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.r为已知,求:
在桌面上有一个倒立的透明的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.r为已知,求:(1)通过计算说明光线1能不能在圆锥的侧面B点发生全反射?
(2)光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是t多少?光照亮地面的光斑面积s多大?
分析:(1)当半径为r的圆柱形平行光束垂直入射到圆锥的地面上,经过第一次折射时,由于入射角等于零,所以折射角也是零,因此折射光线不发生偏折.当第二次折射时,由于入射角等于60°,而玻璃的折射率为1.73,可得入射角与临界角的大小,所以会发生光的全反射,反射光线却恰好垂直射出.
(2)可根据几何关系可确定光线在圆锥内和外通过的路程,由v=
求出光线在玻璃中的速度,即可求解时间.可先根据几何关系可确定光斑的半径,再求解光斑面积.
(2)可根据几何关系可确定光线在圆锥内和外通过的路程,由v=
| c |
| n |
解答: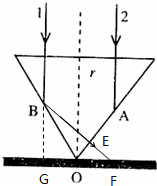 解:(1)设玻璃圆锥的临界角为C,则,由sinC=
解:(1)设玻璃圆锥的临界角为C,则,由sinC=
得:C=arcsin
=arcsin
≈arcsin
而arcsin
=60°
所以C<60°
根据几何知识可知,光线在B点的入射角为60°,大于临界角,所以光线1能在圆锥的侧面B点发生全反射.
(2)由几何关系知:BE=EF=BOtan60°,BO=r
则BE=EF=
r
所以光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是 t=
+
=
+
=
+
=
.
光斑半径 R=OF=GF-BOcos60°=2BEcos30°-r=
r?
-r=2r
故光照亮地面的光斑面积s=πR2=4πr2.
答:
(1)通过计算说明光线1能在圆锥的侧面B点发生全反射.
(2)光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间t为
,光照亮地面的光斑面积s是4πr2.
 解:(1)设玻璃圆锥的临界角为C,则,由sinC=
解:(1)设玻璃圆锥的临界角为C,则,由sinC=| 1 |
| n |
| 1 |
| n |
| 1 |
| 1.73 |
| ||
| 3 |
而arcsin
| ||
| 2 |
所以C<60°
根据几何知识可知,光线在B点的入射角为60°,大于临界角,所以光线1能在圆锥的侧面B点发生全反射.
(2)由几何关系知:BE=EF=BOtan60°,BO=r
则BE=EF=
| 3 |
所以光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是 t=
| BE |
| v |
| EF |
| c |
| BE | ||
|
| EF |
| c |
| ||
| c |
| ||
| c |
2.73
| ||
| c |
光斑半径 R=OF=GF-BOcos60°=2BEcos30°-r=
| 3 |
| 3 |
故光照亮地面的光斑面积s=πR2=4πr2.
答:
(1)通过计算说明光线1能在圆锥的侧面B点发生全反射.
(2)光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间t为
2.73
| ||
| c |
点评:本题关键之处是借助于光的折射与反射定律作出光路图,同时利用几何关系来辅助计算.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
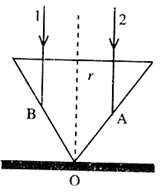
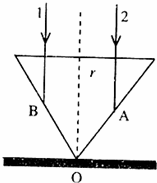
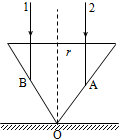 在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r=0.1m的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.则:
在桌面上有一个倒立的玻璃圆锥,其顶点恰好与桌面接触,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,如图所示.有一半径为r=0.1m的圆柱形平行光束垂直入射到圆锥的桌面上,光束的中心轴与圆锥的轴重合.已知玻璃的折射率为n=1.73.则: