题目内容
如图所示，有一半径为r的导电圆环处于磁感应强度为B的匀强磁场中，磁场方向垂直纸面向里且与圆环平面垂直，圆环的电阻为R．若磁感应强度B在时间△t内均匀减小至零，则此过程（ ）分析：根据法拉第电磁感应定律求出线圈中感应电动势．
根据欧姆定律求出感应电流．
根据电量的表达式求出流过圆环截面的电量．
根据电功率的表达式判断功率的变化．
根据欧姆定律求出感应电流．
根据电量的表达式求出流过圆环截面的电量．
根据电功率的表达式判断功率的变化．
解答：解：A、根据法拉第电磁感应定律得：
E=
=
由于磁感应强度B在时间△t内均匀减小至零，
=
，S=πr2，n=1．
所以E=
，I=
=
故A正确．
B、流过圆环截面的电量q=It=
?△t=
．故B正确．
C、在匀强磁场中任何闭合载流回路所受的安培力为零，故C错误．
D、圆环的发热功率P=I2R，从以上分析我们知道，感应电流I不变，电阻R不变，根据P的表达式知道圆环的发热功率不变．故D错误．
故选AB．
E=
| n?△Φ |
| △t |
| n?△B?S |
| △t |
由于磁感应强度B在时间△t内均匀减小至零，
| △B |
| △t |
| B |
| △t |
所以E=
| Bπr2 |
| △t |
| E |
| R |
| Bπr2 |
| R△t |
B、流过圆环截面的电量q=It=
| Bπr2 |
| R△t |
| Bπr2 |
| R |
C、在匀强磁场中任何闭合载流回路所受的安培力为零，故C错误．
D、圆环的发热功率P=I2R，从以上分析我们知道，感应电流I不变，电阻R不变，根据P的表达式知道圆环的发热功率不变．故D错误．
故选AB．
点评：要能够把法拉第电磁感应定律与电路知识结合运用．
求电量时，如果是变化的电流，我们应该取平均电流．
求电量时，如果是变化的电流，我们应该取平均电流．
练习册系列答案
相关题目
如图所示，有一半径为R质量为m的半球形凹槽P，放在光滑的水平地面上，一面紧靠在光滑的墙壁上，在槽口正上方某处有一质量为m的小球，由静止释放，落下后可沿光滑的球面滑下．试问：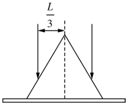
（2012?湖南模拟）桌面上有一玻璃圆锥，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，此三角形的边长为L，如图所示，有一半径为
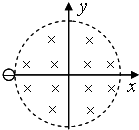如图所示，有一半径为R、有明显边界的圆形匀强磁场区域，磁感应强度为B．今有一电子沿x轴正方向射入磁场，恰好沿y轴负方向射出．如果电子的荷质比为
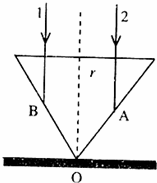在桌面上有一个倒立的透明的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示．有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上，光束的中心轴与圆锥的轴重合．已知玻璃的折射率为n=1.73．r为已知，求：