Question

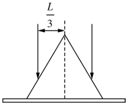（2012?湖南模拟）桌面上有一玻璃圆锥，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，此三角形的边长为L，如图所示，有一半径为

L

3

的圆柱形平行光束垂直底面入射到圆锥上，光束的中心轴与圆锥的轴重合．巳知玻璃的折射率为

3

，求：
①光在玻璃中的传播速度是多少？
②光束在桌面上形成的光斑的面积是多少？

Answer 1

分析：①由v=

c

n

求出光在玻璃中的传播速度．
②作出光路图，根据折射定律求出折射角，由几何关系求出光斑的直径，再求解光斑的面积．

解答：解：①由n=

c

v

得，光在玻璃中的传播速度为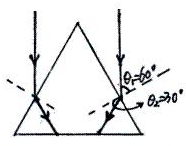
v=

c

n

=

3×108

3

m/s=

3

×108m/s
（2）作出光路图，如图所示．由几何知识得到：入射角θ₁=60°，
根据折射定律得：n=

sinθ1

sinθ2

，代入解得，折射角θ₂=30°．
由几何关系可知，产生的光斑直径为d=

L

3

，面积S=

1

4

πd2=

πL2

36

．
答：
①光在玻璃中的传播速度是

3

×108m/s．
②光束在桌面上形成的光斑的面积是

πL2

36

．

点评：几何光学作出光路图是解答的基础，要规范作出光路图，结合几何知识求解．