题目内容
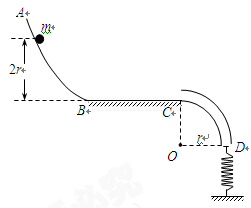
如图所示为某同学设计的节能运输系统.斜面轨道的倾角为37°,木箱与轨道之间的动摩擦因数μ=0.25.设计要求:木箱在轨道顶端时,自动装货装置将质量m=2.8kg的货物装入木箱,木箱载着货物沿轨道无初速滑下,当轻弹簧被压缩至最短时,自动装货装置立刻将货物卸下,然后木箱恰好被弹回到轨道顶端,接着再重复上述过程.若g取10 m/s2,sin37°=0.6 ,cos37°=0.8.求:满足设计要求的木箱质量.

解析试题分析:方法一、对上滑和下滑整个过程运用动能定理,弹簧弹力在整个过程中不做功,最终只有货物重力做功和摩擦力做功,设木箱的质量为 ,下滑的总高度为
,下滑的总高度为 ,全过程用动能定理有
,全过程用动能定理有
代入数据解得: .
.
方法二、在下滑过程中,木箱和货物的重力势能转化为弹簧的弹性势能以及摩擦产生的内能,上滑过程和下滑过程弹性势能相等.设木箱沿轨道下滑的最大距离为L,弹簧被压缩至最短时的弹性势能为 ,根据能量守恒定律:
,根据能量守恒定律:
在木箱与货物一起向下滑到卸货过程中,则有:
卸下货后,木箱被弹回轨道顶端,有
联立代入数据解得:
考点:本题主要考查运用功能关系、能量守恒定律分析和解决物理问题的能力.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案如图甲所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球落到弹簧上压缩弹簧到最低点,然后又被弹起离开弹簧,上升到一定高度后再下落,如此反复.通过安装在弹簧下端的压力传感器,测出这一过程弹簧弹力F随时间t变化的图象如图乙所示,则( )
| A.t1时刻小球动能最大 |
| B.t2时刻小球动能最大 |
| C.t2~t3这段时间内,小球的动能先增加后减少 |
| D.t2~t3这段时间内,小球增加的动能等于弹簧减少的弹性势能 |
质量为m的小球,以速度v斜向上抛离高为H的桌面,如图.取桌面为零势面,那么小球经过离地高度为h的A点时所具有的机械能是
A.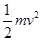 +mg(H-h) +mg(H-h) | B.mgH+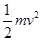 |
C.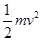 | D.mgH |
如图所示一轻质弹簧下端悬挂一质量为m的小球,用手托着,使弹簧处于原长,放手后,弹簧被拉至最大形变过程中,下列说法正确的是( )
| A.小球先失重后超重 |
| B.小球机械能守恒 |
| C.小球所受的重力做的功大于弹簧的弹力对小球所做的功 |
| D.弹簧被拉至最大形变时,弹簧的弹性势能、小球的重力势能之和最大 |

 的质点距离质量为M0的引力源中心为
的质点距离质量为M0的引力源中心为 时。其引力势能
时。其引力势能 (式中G为引力常数)。现有一颗质量为
(式中G为引力常数)。现有一颗质量为 的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从
的人造地球卫星以圆形轨道环绕地球飞行,由于受高空稀薄空气的阻力作用,卫星的圆轨道半径从 缓慢减小到
缓慢减小到 。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、
。已知地球的半径为R,地球表面的重力加速度为g,求此过程中卫星克服空气阻力做功。(用m、R、g、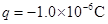 的点电荷由A点沿水平线移至B点,克服静电力做了
的点电荷由A点沿水平线移至B点,克服静电力做了 的功,已知A、B间的距离为
的功,已知A、B间的距离为 。
。
 ,试求B点的电势
,试求B点的电势 ;
;