题目内容
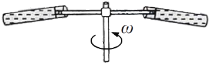
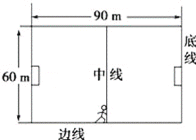
【题目】足球比赛中,经常使用“边路突破,下底传中”的战术,即攻方队员带球沿边线前进,到底线附近进行传中,某足球场长 90m、宽 60m,如图所示,攻方前锋在中线处将足球沿边线 向前踢出,足球的运动可视为在地面上做初速度为12m/s的匀减速直线运动,加速度大小为2m/s2,试求:
(1)足球从开始做匀减速直线运动到停下来的位移为多大;
(2)足球开始做匀减速直线运动的同时,该前锋队员在边线中点处沿边线向前追赶足球, 他的启动过程可以视为从静止出发,加速度为 2m/s2 的匀加速直线运动,他能达到的最大速度为8m/s,该前锋队员至少经过多长时间能追上足球;
(3)若该前锋队员追上足球后,又将足球以速度![]() 沿边线向前踢出,足球的运动仍视为加速度大小为 2m/s2的匀减速直线运动,与此同时,由于体力的原因,该前锋队员以6m/s的速度做匀速直线运动向前追赶足球,若该前锋队员恰能在底线追上足球,则
沿边线向前踢出,足球的运动仍视为加速度大小为 2m/s2的匀减速直线运动,与此同时,由于体力的原因,该前锋队员以6m/s的速度做匀速直线运动向前追赶足球,若该前锋队员恰能在底线追上足球,则![]() 多大。
多大。
【答案】(1) 36m (2) 6.5s (3) 7.5m/s
【解析】
(1)已知足球的初速度为![]() ,加速度大小为
,加速度大小为![]() ,足球做匀减速运动的时间为:
,足球做匀减速运动的时间为:
![]()
由![]()
得到:
![]() ;
;
(2)已知该前锋队员的加速度为![]() ,最大速度为
,最大速度为![]() ,前锋队员做匀加速运动达到最大速度的时间和位移分别为:
,前锋队员做匀加速运动达到最大速度的时间和位移分别为:
![]() ,
,![]()
得到:
![]()
之后前锋队员做匀速直线运动,到足球停止运动时,其位移为:
![]()
由于![]() ,故足球停止运动时,前锋队员没有追上足球,然后前锋队员继续以最大速度匀速运动追赶足球,由匀速运动公式得:
,故足球停止运动时,前锋队员没有追上足球,然后前锋队员继续以最大速度匀速运动追赶足球,由匀速运动公式得:
![]()
代入数据解得:
![]()
前锋队员追上足球的时间为:
![]() ;
;
(3)此时足球距底线的距离为:
![]()
设前锋队员运动到底线的时间为![]() ,则有:
,则有:
![]()
足球在![]() 时间内发生的位移为:
时间内发生的位移为:
![]()
联立以上各式解得:
![]() 。
。

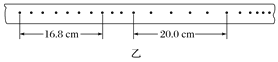
【题目】在做“研究匀变速直线运动”的实验时,某同学得到一条用电火花计时器打下的纸带如图所示,并在其上取了A、B、C、D、E、F、G7个计数点,每相邻两个计数点间还有4个点图中没有画出,电火花计时器接220V、50Hz交流电源.
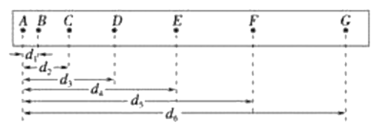
(1)设电火花计时器的周期为T,计算F点的瞬时速度vF的公式为vF=__________;
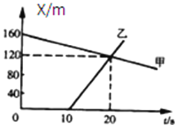
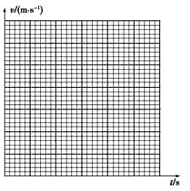
(2)他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表.以A点对应的时刻为t=0,试在下图所示坐标系中合理地选择标度,作出v--t图象______,并利用该图象求出物体的加速度a=_________(保留两位有效数字)
对应点 | B | C | D | E | F |
速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
(3)如果当时电网中交变电流的电压变成210V,而做实验的同学并不知道,那么加速度的测量值与实际值相比______________.(填“偏大”、“偏小”或“不变”)