题目内容
13.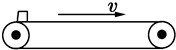 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )| A. | 摩擦力对物体做的功为4J | B. | 摩擦力对物体做的功为-4J | ||
| C. | 电动机做的功为8J | D. | 电动机做功的功率为8W |
分析 物体在摩擦力作用下作匀加速运动,先根据牛顿第二定律求解出加速度,然后假设一直加速,根据运动学公式求出末速度,根据速度时间公式求解出加速时间,摩擦力做的功可以直接用摩擦力乘以物体的位移进行计算,功率等于功除以时间.
解答 解:A、物体放上传送带后先做匀加速直线运动,直到与传送带速度相等,以后做匀速直线运动.
匀加速运动的加速度为:a=$\frac{μmg}{m}$=μg=0.2×10 m/s2=2 m/s2
根据v=at,得:t=$\frac{v}{a}$=$\frac{2}{2}$s=1 s,
物体加速过程的位移为:l1=$\frac{1}{2}$at2=1 m.
摩擦力对物体做正功,有:Wf=μmg•l1=4 J,故A正确,B错误;
C、传送带在1 s内位移为:l2=vt=2 m.则相对位移为:△l=l2-l1=1 m,故系统发热为:Q=Wf′=Ff△l=4 J,
所以电动机做的功为:W=Wf+Q=8 J,故C正确;
D、电动机做功的功率为:P=$\frac{W}{t}$=$\frac{8}{1}$W=8 W,故D正确;
故选:ACD
点评 本题关键要对滑块受力分析后,根据牛顿第二定律求解出加速度,再结合运动学公式以及恒力做功公式列式求解.

练习册系列答案
相关题目
1.关于重心,下列说法正确的是( )
| A. | 重心就是物体内最重的一点 | |
| B. | 物体发生形变时,其重心位置一定不变 | |
| C. | 物体升高或降低时,重心在物体上的位置也相应升高或降低 | |
| D. | 物体的重心可能位于物体之外 |
8.从同一高度以相同的速率分别抛出质量相等的三个小球,一个竖直上抛,一个竖直下抛,另一个平抛,则它们从抛出到落地的过程中( )
| A. | 运行的时间相等 | B. | 位移相同 | ||
| C. | 落地时的速度相同 | D. | 落地时的动能相等 |
18.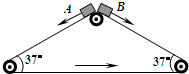 如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是(g取10m/s2,sin37°=0.6,cos37°=0.8)( )
如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是(g取10m/s2,sin37°=0.6,cos37°=0.8)( )
 如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是(g取10m/s2,sin37°=0.6,cos37°=0.8)( )
如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是(g取10m/s2,sin37°=0.6,cos37°=0.8)( )| A. | 物块A先到达传送带底端 | |
| B. | 物块A、B同时到达传送带底端 | |
| C. | 物块A、B在传送带上的划痕长度之比为1:3 | |
| D. | 传送带对物块A、B均做负功,但B克服摩擦力做的功较多 |
5.物体做匀加速直线运动,在第一个时间T内通过位移x1到达A点,接着在第二个时间T内通过位移x2到达B点,第三个时间T末到达C点,则物体( )
| A. | 在A点的速度大小为$\frac{{x}_{1}+{x}_{2}}{2T}$ | B. | 在B点的速度大小为$\frac{2{x}_{2}-{x}_{1}}{2T}$ | ||
| C. | 运动的加速度为$\frac{2{x}_{1}}{{T}^{2}}$ | D. | 在第三个时间T内的位移为3x2-2x1 |
2. (单选)将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
(单选)将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
 (单选)将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
(单选)将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )| A. | $\sqrt{3}$mg | B. | Mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | mg |
3.关于物理学的研究方法,以下说法错误的是( )
| A. | 伽利略开创了运用逻辑推理和实验相结合进行科学研究的方法 | |
| B. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了放大法 | |
| C. | 电场强度是用比值法定义的,因而电场强度与电场力成正比,与试探电荷的电量成反比 | |
| D. | “平均速度”、“总电阻”、“交流电的有效值”用的是“等效替代”的方法 |
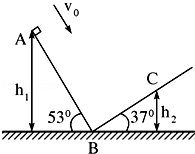 “嫦娥一号”探月卫星的成功发射,实现了中华民族千年奔月的梦想.假若我国的航天员登上某一星球并在该星球表面上做了如图所示力学实验:让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,到达B点后恰好能沿倾角为37°的斜面到达C点.不计滑过B点时的机械能损失,滑块与斜面间的动摩擦因数均为μ=0.5,测得A、C两点离B点所在水平面的高度分别为h1=1.2m,h2=0.5m.已知sin37°=0.6,cos37°=0.8,不计该星球的自转以及其他星球对它的作用.
“嫦娥一号”探月卫星的成功发射,实现了中华民族千年奔月的梦想.假若我国的航天员登上某一星球并在该星球表面上做了如图所示力学实验:让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,到达B点后恰好能沿倾角为37°的斜面到达C点.不计滑过B点时的机械能损失,滑块与斜面间的动摩擦因数均为μ=0.5,测得A、C两点离B点所在水平面的高度分别为h1=1.2m,h2=0.5m.已知sin37°=0.6,cos37°=0.8,不计该星球的自转以及其他星球对它的作用.