题目内容
1.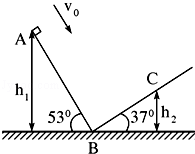 “嫦娥一号”探月卫星的成功发射,实现了中华民族千年奔月的梦想.假若我国的航天员登上某一星球并在该星球表面上做了如图所示力学实验:让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,到达B点后恰好能沿倾角为37°的斜面到达C点.不计滑过B点时的机械能损失,滑块与斜面间的动摩擦因数均为μ=0.5,测得A、C两点离B点所在水平面的高度分别为h1=1.2m,h2=0.5m.已知sin37°=0.6,cos37°=0.8,不计该星球的自转以及其他星球对它的作用.
“嫦娥一号”探月卫星的成功发射,实现了中华民族千年奔月的梦想.假若我国的航天员登上某一星球并在该星球表面上做了如图所示力学实验:让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,到达B点后恰好能沿倾角为37°的斜面到达C点.不计滑过B点时的机械能损失,滑块与斜面间的动摩擦因数均为μ=0.5,测得A、C两点离B点所在水平面的高度分别为h1=1.2m,h2=0.5m.已知sin37°=0.6,cos37°=0.8,不计该星球的自转以及其他星球对它的作用.(1)求该星球表面的重力加速度g;
(2)若测得该星球的半径为R=6×106m,宇航员要在该星球上发射一颗探测器绕其做匀速圆周运动,则探测器运行的最大速度为多大?
(3)取地球半径R0=6.4×106m,地球表面的重力加速度g0=10m/s2,求该星球的平均密度与地球的平均密度之比$\frac{ρ}{{ρ}_{0}}$.
分析 (1)小滑块从A到C的过程中,对滑块进行受力分析和做功分析,根据动能定理列方程求得重力加速度;
(2)根据万有引力提供向心力、重力等于万有引力列式,求解探测器的最大速度.
(3)根据密度公式和黄金代换式GM=gR2,求解星球的平均密度与地球的平均密度之比.
解答 解:(1)小滑块从A到C的过程中,由动能定理得:
mg(h1-h2)-μmgcos53°•$\frac{{h}_{1}}{sin53°}$-μmgcos37°•$\frac{{h}_{2}}{sin37°}$=0-$\frac{1}{2}m{v}_{0}^{2}$
代人数据解得:g=6m/s2
(2)设探测器质量为m′,探测器绕该星球表面做匀速圆周运动时运行速度最大,由牛顿第二定律和万有引力定律得:
G$\frac{Mm′}{{R}^{2}}$=m′$\frac{{v}^{2}}{R}$
又在星球表面有:G$\frac{Mm}{{R}^{2}}$=mg
解得:v=$\sqrt{gR}$
代入数值解得:v=6000m/s=6km/s
(3)由星球密度 ρ=$\frac{M}{\frac{4}{3}π{R}^{3}}$和GM=gR2得该星球的平均密度与地球的平均密度之比为:
$\frac{ρ}{{ρ}_{0}}$=$\frac{g{R}_{0}}{{g}_{0}R}$
代入数值,解得:$\frac{ρ}{{ρ}_{0}}$=0.64.
答:(1)该星球表面的重力加速度为6m/s2;
(2)探测器运行的最大速度为6km/s.
(3)该星球的平均密度与地球的平均密度之比为0.64.
点评 本题是万有引力应用问题,主要从万有引力提供圆周运动的向心力和星球表面重力和万有引力相等两方面入手分析.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
8.质量为m=2kg的物体在光滑的水平面上运动,在水平面上建立xoy坐标系,t=0时,物体位于坐标系的原点O,物体在x轴和y轴方向上的分速度 vx、vy随时间t变化的图象如图甲、乙所示,则下列说法中正确的是( )

| A. | 物体所受的合力是3N | B. | 物体的初速度是3m/s | ||
| C. | 物体做的一定是直线运动 | D. | 物体做的一定曲线运动 |
9.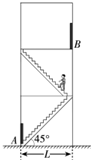 如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )
如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )
 如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )
如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )| A. | 2L | B. | $\sqrt{2}$L | C. | $\sqrt{3}$L | D. | $\sqrt{5}$L |
6. 如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了$\frac{3}{4}$mgh | B. | 克服摩擦力做功$\frac{1}{4}$mgh | ||
| C. | 动能损失了$\frac{3}{4}$mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
13. 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )| A. | 摩擦力对物体做的功为4J | B. | 摩擦力对物体做的功为-4J | ||
| C. | 电动机做的功为8J | D. | 电动机做功的功率为8W |
11.北京奥运会运动项目图标如图所示,形象表现出运动项目的特征,依据图标所做出的判断中,错误的是( )


| A. | 箭被射出的过程中,弹性势能转化为动能 | |
| B. | 游泳的人用力划水时,受到水的推力而前进 | |
| C. | 人举起杠铃在空中停留的几秒钟时间里,人对杠铃做了功 | |
| D. | 曲棍球的运动状态改变,是力作用的结果 |
 如图所示,S为一离子源,MN为荧光屏,足够长,S到MN的距离为SP=L,P为MN的中点,整个装置处在足够大的匀强磁场中,磁感应强度大小为B,方向垂直纸面向里.某时刻离子源S一次性沿平行纸面的各个方向均匀地喷发大量的正离子,此后不再喷发.喷发的离子速率均相等、质量均为m、电荷量均为q,不考虑离子之间的相互作用力及一切阻力.
如图所示,S为一离子源,MN为荧光屏,足够长,S到MN的距离为SP=L,P为MN的中点,整个装置处在足够大的匀强磁场中,磁感应强度大小为B,方向垂直纸面向里.某时刻离子源S一次性沿平行纸面的各个方向均匀地喷发大量的正离子,此后不再喷发.喷发的离子速率均相等、质量均为m、电荷量均为q,不考虑离子之间的相互作用力及一切阻力.