题目内容
18.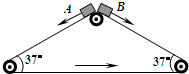 如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是(g取10m/s2,sin37°=0.6,cos37°=0.8)( )
如图所示,三角形传送带以1m/s的速度逆时针匀速转动,两边的传送带长都是2m且与水平方向的夹角均为37°,现有两个小物块A、B从传送带顶端都以1m/s的初速度沿传送带下滑,物块与传送带间的动摩擦因数都是0.5,下列说法正确的是(g取10m/s2,sin37°=0.6,cos37°=0.8)( )| A. | 物块A先到达传送带底端 | |
| B. | 物块A、B同时到达传送带底端 | |
| C. | 物块A、B在传送带上的划痕长度之比为1:3 | |
| D. | 传送带对物块A、B均做负功,但B克服摩擦力做的功较多 |
分析 分析A重力沿斜面向下的分力与摩擦力的关系,判断A物体的运动规律,B所受的摩擦力沿斜面向上,向下做匀变速直线运动,结合牛顿第二定律和运动学公式分析运动时间关系及物块在传送带上的划痕长度之比.根据摩擦力大小和位移关系分析克服摩擦力做功关系.
解答 解:AB、小物块A、B都以1m/s的初速度沿传送带下滑,因为mgsin37°>μmgcos37°,故均沿斜面向下做匀加速直线运动,传送带对两物块的滑动摩擦力均沿斜面向上,大小也相等,则两物块沿斜面向下的加速度大小相同,滑到底端时位移大小相等,故时间相同,故A错误,B正确.
C、由x=v0t+$\frac{1}{2}a{t}^{2}$,a=gsin37°-μgcos37°,得 t=1s,传送带在1s内的位移为 x=vt=1m.A与传送带是同向运动的,A的划痕长度是A对地位移(斜面长度)减去在此时间内传送带的位移,即为 2m-1m=1m.B与传送带是反向运动的,B的划痕长度是B对地位移(斜面长度)加上在此时间内传送带的位移,即为 2m+1m=3m.故C正确.
D、滑动摩擦力方向沿斜面向上,位移沿斜面向下,摩擦力对两物块A、B均做负功,且克服摩擦力做的功一样多,故D错误.
故选:BC
点评 解决本题的关键能正确对其受力分析,判断A、B在传送带上的运动规律,结合运动学公式分析研究.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
5.下列关于摩擦力与物体运动的说法正确的是( )
| A. | 只有运动的物体才会受到滑动摩擦力 | |
| B. | 运动的物体也可能受到静摩擦力 | |
| C. | 摩擦力总是阻碍物体运动,是我们尽量要避免的 | |
| D. | 摩擦力的方向取决于物体运动的方向 |
6.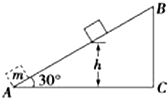 如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度大小为$\frac{3}{4}$g,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了$\frac{3}{4}$mgh | B. | 克服摩擦力做功$\frac{1}{4}$mgh | ||
| C. | 动能损失了$\frac{3}{4}$mgh | D. | 机械能损失了$\frac{1}{2}$mgh |
13.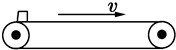 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )| A. | 摩擦力对物体做的功为4J | B. | 摩擦力对物体做的功为-4J | ||
| C. | 电动机做的功为8J | D. | 电动机做功的功率为8W |
7.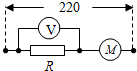 如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
 如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )| A. | 电动机的功率为1100W | |
| B. | 电动机在1分钟内做的机械功为59400J | |
| C. | 电动机在1分钟内发的热为10J | |
| D. | 整个电路在1分钟内发的热为6600J |
8.平行板电容器充电后断开电源,然后将两极板间的正对面积逐渐增大,则在此过程中( )
| A. | 电容逐渐增大 | B. | 极板间场强逐渐增大 | ||
| C. | 极板间电压保持不变 | D. | 极板上电荷量变小 |
 如图所示,斜面倾角θ=30°的光滑斜面上,高h=1m的位置B点,放置一质量为m=1kg的物体.(g取10m/s2)
如图所示,斜面倾角θ=30°的光滑斜面上,高h=1m的位置B点,放置一质量为m=1kg的物体.(g取10m/s2)