题目内容
2. (单选)将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )
(单选)将两个质量均为m的小球a、b用细线相连后,再用细线悬挂于O点,如图所示.用力F拉小球b,使两个小球都处于静止状态,且细线Oa与竖直方向的夹角保持θ=30°,则F达到最小值时Oa绳上的拉力为( )| A. | $\sqrt{3}$mg | B. | Mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | mg |
分析 以两个小球组成的整体为研究对象,当F垂直于Oa线时取得最小值,根据平衡条件利用几何关系可求得oa绳上的拉力.
解答 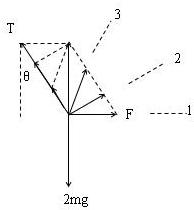 解:以两个小球组成的整体为研究对象,分析受力,作出F在三个方向时整体的受力图,根据平衡条件得知:F与T的合力与重力mg总是大小相等、方向相反,由力的合成图可知,当F与绳子oa垂直时,F有最小值,即图中2位置,
解:以两个小球组成的整体为研究对象,分析受力,作出F在三个方向时整体的受力图,根据平衡条件得知:F与T的合力与重力mg总是大小相等、方向相反,由力的合成图可知,当F与绳子oa垂直时,F有最小值,即图中2位置,
根据平衡条件得F的oa绳上的拉力T=2mgcos30°=$\sqrt{3}$mg;
故选:A
点评 本题是隐含的临界问题,关键运用图解法确定出F的范围,得到F最小的条件,再由平衡条件进行求解.

练习册系列答案
相关题目
9.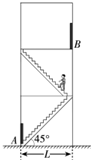 如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )
如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )
 如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )
如图所示,某人沿着倾角为45°的楼梯从一楼A位置走到了二楼B位置,如果楼梯间的宽度为L,则人的位移为( )| A. | 2L | B. | $\sqrt{2}$L | C. | $\sqrt{3}$L | D. | $\sqrt{5}$L |
13. 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
 如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )
如图所示,水平传送带以2m/s的速度匀速运行,现将一质量为2kg的物体轻放在传送带上,物体与传送带间的动摩擦因数为0.2.若不计电动机自身消耗,则将物体传送的过程中( )| A. | 摩擦力对物体做的功为4J | B. | 摩擦力对物体做的功为-4J | ||
| C. | 电动机做的功为8J | D. | 电动机做功的功率为8W |
17.下列叙述正确的是( )
| A. | 重力就是地球对物体的吸引力 | |
| B. | 甲用力把乙推倒而自己不倒,说明只是甲对乙有力的作用,乙对甲没有力的作用 | |
| C. | 在弹性限度内,某一弹簧的弹力与其形变量的比值是常数 | |
| D. | 两物体相互接触,就一定会产生相互作用的弹力 |
7. 如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
 如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )
如图所示,一台电动机M线圈电阻r=0.4Ω,与R=4Ω的电阻串联接在220V的电路中,电动机正常工作.已知理想电压表的示数为20V,以下说法正确的是( )| A. | 电动机的功率为1100W | |
| B. | 电动机在1分钟内做的机械功为59400J | |
| C. | 电动机在1分钟内发的热为10J | |
| D. | 整个电路在1分钟内发的热为6600J |
11.北京奥运会运动项目图标如图所示,形象表现出运动项目的特征,依据图标所做出的判断中,错误的是( )


| A. | 箭被射出的过程中,弹性势能转化为动能 | |
| B. | 游泳的人用力划水时,受到水的推力而前进 | |
| C. | 人举起杠铃在空中停留的几秒钟时间里,人对杠铃做了功 | |
| D. | 曲棍球的运动状态改变,是力作用的结果 |
12.如图所示,顶端装有定滑轮的斜面C放置在粗糙水平面上,A、B两物体通过与斜面C平行的细绳相连,并处于静止状态,不计绳的质量和绳与滑轮间的摩擦,现用水平向右的拉力F作用在物体B上,将物体B缓慢拉高一小段距离,在此过程中斜面C与物体A仍然保持静止,则下列说法正确的是( )

| A. | 斜面C对物体A的摩擦力一定增大 | B. | 斜面C对物体A的摩擦力一定减小 | ||
| C. | 细绳对物体A的作用力可能减小 | D. | 细绳对物体A的作用力一定增大 |