题目内容
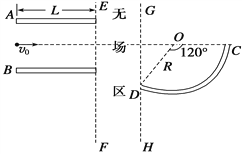
【题目】某兴趣小组设计了一个轨道,依次由光滑曲面![]() 、粗粗水平面
、粗粗水平面![]() 、光滑竖直圆轨道及足够长的倾斜传送带组成,如图所示。滑块从曲面上某位置
、光滑竖直圆轨道及足够长的倾斜传送带组成,如图所示。滑块从曲面上某位置![]() 下滑,沿水平面从
下滑,沿水平面从![]() 点左侧进入圆轨道再从
点左侧进入圆轨道再从![]() 点右侧离开继续向前运动,经过连接点
点右侧离开继续向前运动,经过连接点![]() 时没有机械能损失。已知圆轨道半径
时没有机械能损失。已知圆轨道半径![]() ,
,![]() ,
,![]() ,滑块质量
,滑块质量![]() ,滑块与水平轨道
,滑块与水平轨道![]() 、传送带间动摩擦因数
、传送带间动摩擦因数![]() 均为0.5,传送带与水平面间的夹角
均为0.5,传送带与水平面间的夹角![]() ,以
,以![]() 的速度做逆时针运动。(
的速度做逆时针运动。(![]() )求:
)求:
(1)要使滑块恰好经过圆轨道的最高点,静止释放滑块的高度为多大;
(2)滑块从(1)问中释放位置以初动能![]() 滑下,滑块在传动带上向上运动的时间;
滑下,滑块在传动带上向上运动的时间;
(3)满足(2)问的条件下,滑块最终停在什么位置?

【答案】(1)2.25m(2)0.8s(3)C点右侧0.4m处
【解析】
(1)设滑块下滑高度为![]() 时,恰好经过圆轨道最高点
时,恰好经过圆轨道最高点![]() ,在
,在![]() 点:
点:
![]()
![]() 到
到![]() 由动能定理得
由动能定理得
![]()
解得:
![]()
即释放滑块的高度至少为![]() ,才能顺利经过圆轨道最高点
,才能顺利经过圆轨道最高点![]() 。
。
(2)设滑块运动到![]() 点速度为
点速度为![]() , 由动能定理:
, 由动能定理:
![]()
代入数据得:
![]()
滑块沿传送带向上运动加速度为![]() ,由牛顿第二定律:
,由牛顿第二定律:
![]()
代入数据得:
![]()
向上运动时间:
![]()
代入数据得:
![]()
(3)滑块向上运动最远距离:
![]()
接着滑块沿传送带下滑,加速度仍然是![]() ,和传送带速度相同时运动距离:
,和传送带速度相同时运动距离:
![]()
因为![]() ,此后滑块继续向下加速,设滑块在圆轨道能上升高度为
,此后滑块继续向下加速,设滑块在圆轨道能上升高度为![]()
由动能定理得:
![]()
代入数据得:
![]() ,
,
因此滑块返回到![]() 点右侧,设其运动距离为
点右侧,设其运动距离为![]() ,由:
,由:
![]()
代入数据得:
![]()
滑块最着能终停在![]() 点右侧
点右侧![]() 处。
处。

练习册系列答案
相关题目