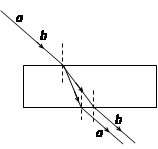题目内容
如下图所示,一束光线以60°的入射角射到一水平放置的平面镜上,反射后在正上方与平面镜平行的光屏上留下一光点P.现将一块上下两面平行的透明体平放在平面镜上,如图中虚线所示,则进入透明体的光线经平面境反射后再从透明体的上表面射出,打在光屏上的光点P′,与原来相比向左平移了3.46 cm,已知透明体对光的折射率为.
(1)作出后来的光路示意图,标出P′位置;
(2)透明体的厚度为多大?
(3)光在透明体里运动的时间多长?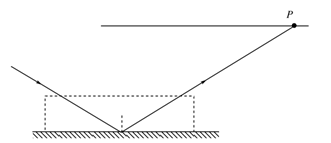
(1)作出后来的光路示意图,标出P′位置;
(2)透明体的厚度为多大?
(3)光在透明体里运动的时间多长?

(1)见解析(2) 2×10-10 s
(1)光路图如下图所示.
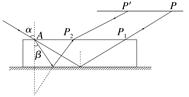
(2)由折射定律sin α=nsin β代入数据解得:
β=30°
设透明体的厚度为d
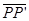 =
=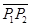 =
=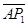 -
-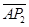 =2dtan α-2dtan β
=2dtan α-2dtan β
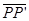 =2
=2 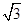 d-
d-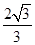 d=2
d=2 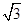 cm
cm
d=1.5 cm.
(3)光在透明体里运动的速度:v=
光在透明体里运动的路程:s=2·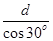
光在透明体里运动的时间是: t=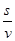 =
=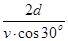 =
=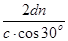 =2×10-10 s.
=2×10-10 s.
本题考查折射定律,根据光路图、折射定律求出角度大小,再由几何关系求出运动时间

(2)由折射定律sin α=nsin β代入数据解得:
β=30°
设透明体的厚度为d
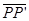 =
=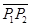 =
=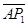 -
-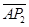 =2dtan α-2dtan β
=2dtan α-2dtan β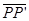 =2
=2 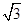 d-
d-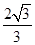 d=2
d=2 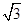 cm
cmd=1.5 cm.
(3)光在透明体里运动的速度:v=

光在透明体里运动的路程:s=2·
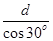
光在透明体里运动的时间是: t=
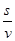 =
=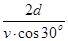 =
=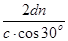 =2×10-10 s.
=2×10-10 s.本题考查折射定律,根据光路图、折射定律求出角度大小,再由几何关系求出运动时间

练习册系列答案
相关题目

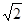 ,若要使油量计能正常工作,问透明塑料的折射率n应满足怎样的条件?
,若要使油量计能正常工作,问透明塑料的折射率n应满足怎样的条件?
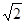 .一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出.
.一束与MN平面成450的平行光束射到玻璃砖的半圆柱面上,经玻璃折射后,有部分光能从MN平面上射出. (2)如果平行光束是以45°角从空气射到半圆柱的平面表面上,如图2所示,设此时从半圆柱面上出射光束的位置与圆心O的连线跟MO夹角为φ,试求φ的范围.
(2)如果平行光束是以45°角从空气射到半圆柱的平面表面上,如图2所示,设此时从半圆柱面上出射光束的位置与圆心O的连线跟MO夹角为φ,试求φ的范围.