题目内容
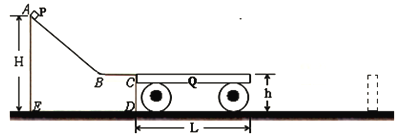
【题目】如图所示，高H=2．4m的赛台ABCDE固定于地面上，其上表面ABC光滑；质量M=2kg、高h=0．6m、长L的小车Q紧靠赛台右侧CD面（不粘连），放置于光滑水平地面上。质量m=1kg的小物块P从赛台顶点A由静止释放，经过B点的小曲面无损失机械能的滑上BC水平面，再滑上小车的左端。已知小物块与小车上表面的动摩擦因数μ=0．3，g取10m/s2。
（1）求小物块P滑上小车左端时的速度v1；
（2）如果小物块没有从小车上滑脱，求小车最短长度L0；
（3）若小车长L=4．5m，距离小车右端S处有与车面等高的竖直挡板，小车碰上挡板后立即停止不动，讨论小物块在小车上运动过程中，克服摩擦力做功Wf与S的关系。
【答案】（1）6m/s（2）4m（3）若
， 
；若
【解析】试题分析：物块从P到A过程机械能守恒，应用机械能守恒定律可以求出速度．物块与小车系统动量守恒，应用动量守恒定律与能量守恒定律可以求出车的长度．根据s与小车位移的关系，应用动能定理求出摩擦力的功与s的关系．
（1）小物块P从A滑到B点的过程中机械能守恒，
由机械能守恒定律得： 
，
代入数据解得
（2）小物块P在小车Q的上表面滑动的过程中，P、Q构成的系统所受合外力为零，系统动量守恒，取小车最短长度
时，小物块刚好在小车右端共速为
．
以向右为正方向，由动量守恒定律得： 
①
相对运动过程中系统的能量守恒，有： 
②
联立并代入已知数据解得： 
；
（3）小车长L=4.5m，说明小车与竖直挡板相撞前小物块不会滑脱小车，
设共速时小车位移
，物块对地位移
，
分别对小车和物块由动能定理可知
， 
，
代入数据解得： 
；
①若
，说明小车与挡板碰撞前小物块与小车已具有共同速度，且共速后一起匀速至挡板处，小物块将在小车上继续向右做初速度为
的匀减速运动，
距离车尾位移为
，设减速到0位移为，则
，
可得
，则小物块在车上飞出去， 
，
代入数据解得
；
②若
，说明小车与挡板碰撞前小物块与小车还没有共速，小物块全程都受摩擦力作用，则
，代入数据解得
；
