��Ŀ����
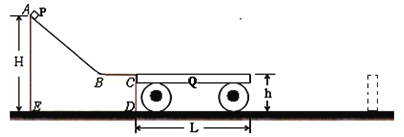
����Ŀ����ͼ��һ�ᵯ���¶����������Ϊ30��Ĺ̶�б���ϣ�һ����Ϊ1kg�Ļ��飨����Ϊ�ʵ㣩��б�涥��a���ɾ�ֹ��ʼ�»�����b��Ӵ����ɣ����齫����ѹ������͵�c��Ȼ���ֻص�a�㣮��֪ab��������Ϊ0.8m��bc��������Ϊ0.2m���������ٶ�gȡ10m/s2 �� ����˵����ȷ���ǣ� ��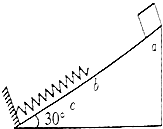
A.��a���һ���˶���b��Ĺ����У�����Ļ�е���غ�
B.��b���˶���c��Ĺ����У������������ܵļ��������ڵ��ɵ������ܵ�������
C.���������е��ɵ������ܵ����ֵΪ5J
D.���������л��鶯�ܵ����ֵΪ5J
���𰸡�A,C
���������⣺A������֪�����鱻���ɵ��غ��ܻص�a�㣬˵��б���ǹ⻬�ģ����a���һ���˶���b��Ĺ����У�ֻ����������������Ļ�е���غ㣬��A��ȷ��
B����b���˶���c��Ĺ����У�����Ķ��ܺ��������ܶ����٣����ɵĵ����������ӣ����ڵ��ɺͻ�����ɵ�ϵͳֻ�������͵�������������ϵͳ�Ļ�е���غ㣬��֪�ù����У������������ܵļ������붯�ܼ�����֮�͵��ڵ��ɵ������ܵ�����������B����
C�������a��c�����ö��ܶ����ã�mghac+W����=0��0���� hac=Sacsin30��=0.5m
��ã�W����=��5J��
���ɵ������Ĺ����ڵ������ܵı仯���ĸ�ֵ���������������е��ɵ������ܵ����ֵΪ5J����C��ȷ��
D��������ĺ���Ϊ0ʱ�������ٶ�����軬����d�����Ϊ0��d����b��c֮�䣮�����a��d�����ö��ܶ����ã�mghad+W��=EKd��0
mghad��mghac=10��0.5J=5J��W����0�����Զ��ܵ����ֵ EKd��5J����D����
��ѡ��AC
�����㾫�������չ��ܹ�ϵ�ǽ����ĸ�������Ҫ֪����ֻ���������ɵ���������ʱ������Ļ�е���غ㣻�������������Ĺ����������������ܵļ���:W G =E p1 -E p2�������������������Ĺ��������嶯�ܵı仯:W �� =E k2 -E k1 �����ܶ������������������ɵ�����֮����������������Ĺ����������е�ܵı仯:W F =E 2 -E 1��

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д�