题目内容
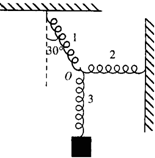
质量为m,带电量为+q的小物体在O点以初速度v0沿与水平成30°角方向射出.如图所示,物体在运动过程中,除重力外,还受到方向始终与初速度v0方向相反的力F的作用.
(1)若F=mg,要使物体保持v0做匀速直线运动,可在某一方向加上一定大小的匀强电场,求此电场强度的大小和方向.
(2)若F=2mg,且电场强度的大小与(1)中相同,仍要使物体沿v0方向做直线运动,那么该电场强度的可能方向如何?求出物体沿入射方向的最大位移和回到O点的最短时间及回到O点的速度大小?

(1)若F=mg,要使物体保持v0做匀速直线运动,可在某一方向加上一定大小的匀强电场,求此电场强度的大小和方向.
(2)若F=2mg,且电场强度的大小与(1)中相同,仍要使物体沿v0方向做直线运动,那么该电场强度的可能方向如何?求出物体沿入射方向的最大位移和回到O点的最短时间及回到O点的速度大小?

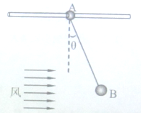
(1)设所加场强E的方向与初速度成θ角,如图所示,则
qEsinθ=mgcos30°
qEcosθ=F+mgsin30°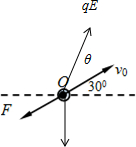
且F=mg
得θ=30°,E=
(2)设场强E与初速度夹角为a,要使物体做直线运动只须:
qEsina=mgcos30°得a=30°或150°
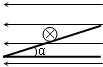
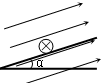
1)当a=30°时,物体的加速度最小,沿初速度方向的位移最大,受力如上图所示.
由牛顿第二定律,有:
F+mgsin30°-qEcos30°=ma1
又由运动学公式知:
=2a1s
其中:F=2mg,E=
可得S=
2)当a=150°时,物体的加速度最大,回到O点时的时间最短,受力如图所示.由牛顿第二定律,有
F+mgsin30°+qEcos30°=ma2
-a2
=0
其中:F=2mg,E=
,可得
回到O点的最短时间t=
回到O点的速度V=V0-a2t=-V0
负号表示与初速度反向
答:(1)此电场强度的大小
,方向与初速度成30°.
(2)该电场强度的可能与初速度成30°或150°,物体沿入射方向的最大位移S=
,回到O点的最短时间
,回到O点的速度大小V0.
qEsinθ=mgcos30°
qEcosθ=F+mgsin30°

且F=mg
得θ=30°,E=
| ||
| q |
(2)设场强E与初速度夹角为a,要使物体做直线运动只须:
qEsina=mgcos30°得a=30°或150°
1)当a=30°时,物体的加速度最小,沿初速度方向的位移最大,受力如上图所示.
由牛顿第二定律,有:
F+mgsin30°-qEcos30°=ma1
又由运动学公式知:
| V | 20 |
其中:F=2mg,E=
| ||
| q |
可得S=
| ||
| 2g |
2)当a=150°时,物体的加速度最大,回到O点时的时间最短,受力如图所示.由牛顿第二定律,有
F+mgsin30°+qEcos30°=ma2
| V | 20 |
| t |
| 2 |
其中:F=2mg,E=
| ||
| q |
回到O点的最短时间t=
| V0 |
| 2g |
回到O点的速度V=V0-a2t=-V0
负号表示与初速度反向
答:(1)此电场强度的大小
| ||
| q |
(2)该电场强度的可能与初速度成30°或150°,物体沿入射方向的最大位移S=
| ||
| 2g |
| V0 |
| 2g |

练习册系列答案
相关题目