题目内容
【题目】一个折射率为![]() 的梯形玻璃砖,已知AD边长为4cm,CD边长为6cm,两底角分别为30°、60°,如图所示。一束单色光(纸面内)从AD边中点E入射,入射角为45°时。已知光速为
的梯形玻璃砖,已知AD边长为4cm,CD边长为6cm,两底角分别为30°、60°,如图所示。一束单色光(纸面内)从AD边中点E入射,入射角为45°时。已知光速为![]() 。
。

①求该单色光从玻璃砖射出时光线与法线的夹角;
②求单色光在玻璃砖内传播时间。
【答案】① 0° ②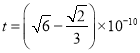 s
s
【解析】
①如图,设光束经折射后到达玻璃砖底面上M点
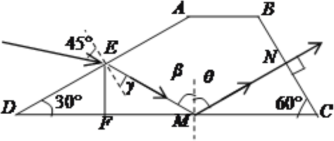
由折射定律:![]()
解得:![]()
由几何关系可知![]()
根据![]() 可知发生全反射的临界角为45°
可知发生全反射的临界角为45°
β>45°,故该单色光在底面M点发生全反射,所以![]()
根据几何关系可知光线沿MN方向垂直BC边界出射,
故该单色光从玻璃砖射出时光线与法线的夹角为0°
②该单色光在玻璃砖内的光路如图所示,因E为AD中点,故DE=2cm,过E点做DC边垂线交DC于F点,在△EDF中可求得EF=1cm,DF=![]() cm,
cm,
由几何关系可知∠EMF=30°,在△EMF中可求得FM=![]() cm,EM=2cm
cm,EM=2cm
所以MC=DC-DF-FM=(![]() )cm,在△MNC中可求得MN=
)cm,在△MNC中可求得MN=![]() cm
cm
根据![]()
求得:![]() m/s
m/s
又S=EM+MN=(![]() )cm,将数据代入
)cm,将数据代入![]()
解得: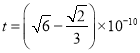 s
s

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目