题目内容
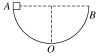
【题目】某同学用如图所示装置，通过半径相同的A、B两球的碰撞来探究动量守恒。测量所得入射球A的质量为mA，被碰撞小球B的质量为mB，图中O点是小球抛出点在水平地面上的垂直投影，实验时，先让入射球A从斜轨上的起始位置由静止释放，找到其平均落点的位置P，测得平抛射程为OP；再将入射球A从斜轨上起始位置由静止释放，与小球B相撞，分别找到球A和球B相撞后的平均落点M、N，测得平抛射程分别为OM和ON。要实现A与B碰撞后不反弹，A、B两球的质量应满足的关系是mA_______mB（填大于、小于或等于），当所测物理量满足表达式__________________时，即说明两球碰撞中动量守恒；如果还满足表达式________________时，则说明两球的碰撞为弹性碰撞。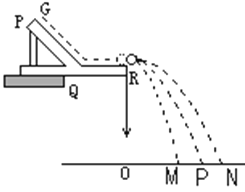
【答案】 大于； mA·OP= mA·OM+ mB·ON； mAOP2=mAOM2+mBON2
【解析】此实验中要实现A与B碰撞后不反弹，A、B两球的质量应满足的关系是mA大于mB；小球离开轨道后做平抛运动，由于小球抛出点的高度相同，它们在空中的运动时间t相等，它们的水平位移x与其初速度成正比，可以用小球的水平位移代替小球的初速度，若两球相碰前后的动量守恒，则mAv0=mAv1+mBv2，又OP=v0t，OM=v1t，ON=v2t，代入得mAOP=mAOM+mBON，
若碰撞是弹性碰撞，则机械能守恒，由机械能守恒定律得： 
mAv02=
mAv12+
mBv22，
将OP=v0t，OM=v1t，ON=v2t代入得：mAOP2=mAOM2+mBON2；
练习册系列答案
相关题目
