��Ŀ����
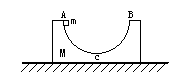
����Ŀ����ͼ��ʾ���ڹ⻬ˮƽ������һ������M=8kg��ƽ��С����������һ������m=1.9kg��ľ�飬ľ���С�����6m��ľ�����Ϊ�ʵ㣩������ľ��һ����v=1m/s���ٶ�ˮƽ����������ʻ��һ������m0=0.1kg���ӵ���v0=179m/s�ij��ٶ�ˮƽ���������˲�����ľ�鲢�������У�����ľ��պò��ӳ��ϵ�����������

��1���ӵ�����ľ���Ĺ�ͬ�ٶ�Ϊv1��
��2��ľ����ƽ��֮��Ķ�Ħ�������̣�g=10m/s2��
���𰸡���1��8m/s��
��2��0.54
��������
�����������1���ӵ���ľ����ɵ�ϵͳ�����غ㣬�ɶ����غ㶨�ɿ������ľ����ٶȣ�
��2���ӵ���ľ�顢С����ɵ�ϵͳ�����غ㣬�ɶ����غ㶨��������ǵĹ�ͬ�ٶȣ�Ȼ���������غ㶨�������Ħ��������
�⣺��1���ӵ�����ľ������У��ӵ���ľ����ɵ�ϵͳ�����غ㣬���ӵ��ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
m0v0��mv=��m0+m��v1��
�������ݽ��ľ�������ٶ�Ϊ��v1=8v=8m/s��
��2�����ӵ���ľ�顢С����ɵ�ϵͳΪ�о��������ӵ��ij��ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
��m0+m��v1��Mv=��m0+m+M��v2��
�������غ㶨�ɵã��̣�m0+m��gL=![]() ��m0+m��v12��
��m0+m��v12��![]() ��m0+m+M��v22��
��m0+m+M��v22��
��������=0.54
�𣺣�1�������������У�ľ�������ٶ�Ϊ8m/s��
��2��ľ����ƽ��С��֮��Ķ�Ħ������Ϊ0.54

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�