题目内容
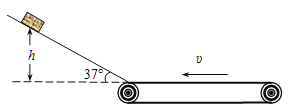
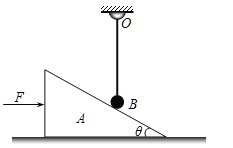
【题目】如图所示，一根长为l=2m的竖直轻杆上端拴在光滑固定转轴O上，下端拴一个小球B，小球B和斜面体A刚好接触．现用水平推力F向右推斜面体，使之从静止开始在光滑水平面上向右运动一段距离，速度达到
，此时轻杆平行于斜面，小球B的速度大小为
，已知斜面体质量为
=4kg，斜面倾角为θ=37°，小球B质量为
=2kg，小球一直未脱离斜面，重力加速度为g=10
，sin37°=0．6，cos37°=0．8，不计空气阻力。
（1）若=15m/s，=9m/s，求在此过程中推力F所做的功；
（2）若轻杆平行于斜面时杆对小球作用力大小
=48N，求此时大小；
（3）若轻杆平行于斜面时=5m/s，求此时大小．
【答案】（1）547J（2）6m/s （3）3m/s
【解析】
试题分析：（1）对整体由功能关系可得：
代入数据得推力所做的功为：
=547J
（2）小球B做圆周运动的向心力由重力的分力和杆的作用力提供，斜面的支持力不提供向心力，此时沿杆方向由牛顿运动定律得：
代入数据得：
=6m/s
（3）根据运动效果可知，将
沿斜面向下方向和垂直于斜面向上方向分解，小球绕悬点O做圆周运动，此时速度大小与垂直于斜面方向的分量相等，这是小球不脱离斜面的条件．由速度的关系可得：=sin37°=3m/s
练习册系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
