题目内容
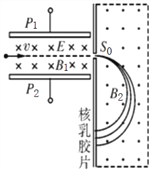
【题目】（16分）如图甲所示，竖直虚线MN、PQ间有垂直于纸面向里的匀强磁场，MN左侧有水平的平行金属板，板的右端紧靠虚线MN，在两板的电极P、Q上加上如图乙所示的电压，在板的左端沿两板的中线不断地射入质量为m，电荷量为+q的带电粒子，粒子的速度均为v0，侧移最大的粒子刚好从板的右侧边缘射入磁场，两板长为L，若
远大于T，磁场的磁感应强度为B，
不计粒子的重力，求：
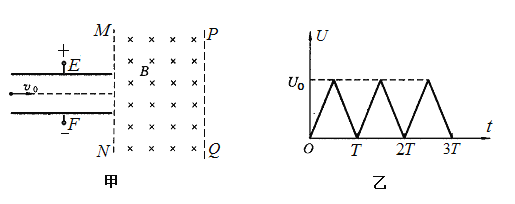
（1）两板间的距离d为多少？
（2）要使所有粒子均不能从边界PQ射出磁场，PQ、MN间的距离至少多大？
（3）若将下板下移
，则所有粒子进入磁场后，要使所有粒子均不能从边界PQ射出磁场，PQ、MN间的距离又至少为多大？
【答案】见解析
【解析】（1）由于
远大于T，因此每个粒子穿过电场时可以认为电场强度大小不变，当两板间的电压为U0时，粒子穿过两板间的侧移最大，设板间距离为d，则
（1分）
（1分）
求得
（2分）
（2）设粒子进磁场时速度与水平方向的夹角为
，则粒子在磁场中运动的速度
（1分）
粒子在磁场中运动时
（1分）
（1分）
粒子在磁场中做圆周运动时，轨迹上点离MN的最远距离
（2分）
可见，
越大，s越大，则从平行板边缘飞出的粒子速度与水平方向夹角最大，此时
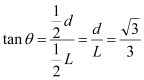（1分）
（1分）
因此PQ、MN间的距离至少为
（1分）
（3）若将下板下移
，则两板间的距离为
（1分）
则所有粒子在电场中的侧移最大值
（1分）
设最大偏向角为α，则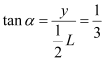
，则
（1分）
因此要使所有粒子均不能从PQ边射出磁场，需要PQ、MN间的距离至少为
（1分）
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
