题目内容
12.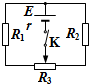 在如图所示电路中,电源电动势E=6.3V,内电阻r=0.50Ω.定值电阻R1=2.0Ω,R2=3.0Ω,R3是最大电阻值为5.0Ω的滑动变阻器.接通开关K,调节滑动变阻器的触点,求通过电源的电流范围和电源输出的最大电功率.
在如图所示电路中,电源电动势E=6.3V,内电阻r=0.50Ω.定值电阻R1=2.0Ω,R2=3.0Ω,R3是最大电阻值为5.0Ω的滑动变阻器.接通开关K,调节滑动变阻器的触点,求通过电源的电流范围和电源输出的最大电功率.
分析 设滑动变阻器与R1并联部分的电阻为R右,根据电路的连接关系,推导出电路总电阻表达式,分析总电阻的最大值和最小值,即由闭合电路欧姆定律求得电源的电流最小值和最大值.由电源输出功率的表达式结合数学规律可明确对应的最大值.
解答 解:设R3中与R1串联的那部分电阻为x,外电路的结构是:x与R1串联、(R3-x)与R2串联,然后这两串电阻再并联.
外电阻为$R=\frac{{({R_1}+x)({R_2}+{R_3}-x)}}{{{R_1}+R'+{R_2}+{R_3}-R')}}=\frac{{({R_1}+x)({R_2}+{R_3}-x)}}{{{R_1}+{R_2}+{R_3}}}$
根据数学知识可知,当两数和为定值时:若两数差值越大则其积越小,两数差值越小则其积越大,两数相等时其积最大.
要使通过电源的电流最小,外电阻应当最大.即当R1+x1=R2+R3-x1时,R最大,
解得x1=3Ω.
外电路最大电阻为${R_大}=\frac{{({R_1}+{x_1})({R_2}+{R_3}-{x_1})}}{{{R_1}+{R_2}+{R_3}}}=\frac{(2+3)(3+5-3)}{2+3+5}Ω=2.5Ω$
通过电源的最小电流为${I_小}=\frac{E}{{{R_大}+r}}=\frac{6.3}{2.5+0.5}V=2.1A$
要使通过电源的电流最大,外电阻应当最小.因为R1=2Ω<R2=3Ω,所以当变阻器滑动头滑到R3左端点时两部分电阻差值最大,此时x2=0时,R最小.
外电路的最小电阻为${R_小}=\frac{{{R_1}({R_2}+{R_3})}}{{{R_1}+{R_2}+{R_3}}}=\frac{2×(3+5)}{2+3+5}Ω=1.6Ω$
通过电源的最大电流为${I_大}=\frac{E}{{{R_小}+r}}=\frac{6.3}{1.6+0.5}V=3.0A$
通过电源的电流范围为2.1A≤I≤3.0A
电源输出的电功率为$P={I^2}R={(\frac{E}{R+r})^2}R=\frac{E^2}{{\frac{{{{(R-r)}^2}}}{R}+4r}}$
外电阻越接近内电阻,电源输出的电功率越大,当外电阻最小时,外电阻最接近于内电阻,此时电源输出的电功率最大,最大输出电功率为${P_大}=I_大^2{R_小}={3.0^2}×1.6W=11.4W$
答:通过电源的电流范围2.1A≤I≤3.0A;电源输出的最大电功率为11.4W.
点评 本题考查功率公式有闭合电路欧姆定律的应用;要注意运用数学上函数法求解极值,考查运用数学知识解决物理问题的能力.

 某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关系.实验室提供如下器材:
某研究性学习小组欲探究光滑斜面上物体下滑的加速度与物体质量及斜面倾角是否有关系.实验室提供如下器材:A.表面光滑的长木板(长度为L);B.小车;C.质量为m的钩码若干个;D.方木块(备用于垫木板);E.米尺;F.秒表.
(1)实验过程:
第一步,在保持斜面倾角不变时,探究加速度与质量的关系.实验中,通过向小车放入钩码来改变物体的质量,只要测出小车由斜面顶端滑至底端所用的时间t,就可以由公式a=$\frac{2L}{{t}^{2}}$求出a,某同学记录了数据如下表所示:
| 质量 时间 t次数 | M | M+m | M+2m |
| 1 | 1.42 | 1.41 | 1.42 |
| 2 | 1.40 | 1.42 | 1.39 |
| 3 | 1.41 | 1.38 | 1.42 |
第二步,在物体质量不变时,探究加速度与倾角的关系.实验中通过改变方木块垫放位置来调整长木板倾角,由于没有量角器,因此通过测量出木板顶端到水平面高度h,求出倾角α的正弦值sinα=$\frac{h}{L}$.某同学记录了高度h和加速度a的对应值如表:
| L(m) | 1.00 | ||||
| h(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| sinα=$\frac{h}{L}$ | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| a(m/s2) | 0.97 | 1.950 | 2.925 | 3.910 | 4.900 |
(2)该探究小组所采用的探究方法是控制变量法.
 伏安法是一种常用的测量导体电阻的方法,某同学分别用如图(a)、(b)两种接法测量一个电阻器的阻值,以下结论正确的是( )
伏安法是一种常用的测量导体电阻的方法,某同学分别用如图(a)、(b)两种接法测量一个电阻器的阻值,以下结论正确的是( )| A. | 用图(a)接法测得的电阻值偏大 | |
| B. | 用图(b)接法测得的电阻值偏大 | |
| C. | 用图中两种接法测得的电阻值都偏大 | |
| D. | 用图中两种接法测得的电阻值都偏小 |

①开关S闭合之前,图甲中滑动变阻器的滑片应该置于A端(选填“A”、“B”或“AB中间”)
②根据电路图甲,用笔画线代替导线,将图乙中的实验电路连接完整.
③实验中测得有关数据如表:
| $\frac{U}{V}$ | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 |
| $\frac{I}{A}$ | 0.10 | 0.16 | 0.20 | 0.23 | 0.25 | 0.26 | 0.27 |
 如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )
如图所示,质量为m的木块放在质量为M的木板上,一起减速向右滑行,木板与地面间动摩擦因数为μ1,木块与木板间动摩擦因数为μ2,木块与木板相对静止,木板受到地面的摩擦力为f1,木板受到木块的摩擦力为f2,则( )| A. | f1=μ1Mgf2=μ1mg | B. | f1=μ1(M+m)gf2=μ1mg | ||
| C. | f1=μ1Mgf2=μ2mg | D. | f1=μ1(M+m)gf2=μ2mg |
| A. | 在落地前的任一时刻,两石块具有相同的速度、位移和加速度 | |
| B. | 重的石块下落得快、轻的石块下落得慢 | |
| C. | 两石块在下落过程中的平均速度相等 | |
| D. | 它们在第1s、第2s、第3s内下落的高度之比为1:3:5 |
 平板车M在水平拉力F控制作用下,始终以v0=4m/s的恒定速度水平向右运动,若在车最右端放一相对地面初速度为零、可视为质点的物体m,则经过2s后物体恰好到达车的正中央,已知车与物体间的动摩擦因数μ=0.1,车与地面间的动摩擦因数是0.2,g=10m/s2.问:
平板车M在水平拉力F控制作用下,始终以v0=4m/s的恒定速度水平向右运动,若在车最右端放一相对地面初速度为零、可视为质点的物体m,则经过2s后物体恰好到达车的正中央,已知车与物体间的动摩擦因数μ=0.1,车与地面间的动摩擦因数是0.2,g=10m/s2.问: 如图所示,CD左侧存在电场强度大小E=$\frac{mg}{q}$、方向水平向左的匀强电场.一个质量为m、电荷量为+q的绝缘小球,从底边BC长为L、倾角为45°的直角三角形斜面顶端A点,以初速度v0开始下滑,运动到斜面底端后由C点进入一竖直光滑的半圆形细管(C处为一小段长度可忽略的光滑圆弧,圆管内径略大于小球直径,半圆直径CD在竖直线上)后,恰能到达细管最高点D点(处于电场中),随后从D点离开后落回斜面上某点P.小球与斜面间的动摩擦因数为u,重力加速度为g,求:
如图所示,CD左侧存在电场强度大小E=$\frac{mg}{q}$、方向水平向左的匀强电场.一个质量为m、电荷量为+q的绝缘小球,从底边BC长为L、倾角为45°的直角三角形斜面顶端A点,以初速度v0开始下滑,运动到斜面底端后由C点进入一竖直光滑的半圆形细管(C处为一小段长度可忽略的光滑圆弧,圆管内径略大于小球直径,半圆直径CD在竖直线上)后,恰能到达细管最高点D点(处于电场中),随后从D点离开后落回斜面上某点P.小球与斜面间的动摩擦因数为u,重力加速度为g,求: 某同学为了探究工程车卸载砂石过程的原理,将此过程等价于粗糙拖斗斜面上放有物块,此斜面倾角可以调节,建立如图所示模型.
某同学为了探究工程车卸载砂石过程的原理,将此过程等价于粗糙拖斗斜面上放有物块,此斜面倾角可以调节,建立如图所示模型.