题目内容
7.现有A、B两列火车在同一轨道上同向行驶,A车在前其速度vA=10m/s,B车在后速度vB=30m/s.因大雾原因,B车司机在距A车350m时才发现前方有车,此时B车司机立即刹车,但要减速1800m才能够停止.求:(1)B车刹车后减速运动的加速度大小
(2)若B车刹车8s后,A车司机发现险情并以加速度a=0.5m/s2加速前进,计算说明能否避免事故.
分析 (1)根据匀变速直线运动位移-速度关系式求出加速度;
(2)当两车速度相等时不会相撞,以后就不会相撞了,设经过时间t两车速度相等,求出时间t,再分别求出AB两车的位移,根据位移明确是否会发生事故.
解答 解:(1)根据2ax=${v}^{2}{{-v}_{0}}^{2}$得;
a=$\frac{0{{-v}_{0}}^{2}}{2s}$=$\frac{-900}{2×1800}$=-0.25m/s2
(2))设B车减速t秒时两车的速度相同:
vB+aBt=vA+aA(t-△t)
代入数值解得:t=32s
在此过程中:SB=vB t+$\frac{1}{2}$aBt2
解得:SB=832 m
SA=vA t+$\frac{1}{2}$aA(t-△t)2
解得:SA=464m
SA+S=350+464=814m<SB
故不能避免事故
答:(1)B车刹车后减速运动的加速度大小为0.25m/s2;(2)若B车刹车8s后,A车司机发现险情并以加速度a=0.5m/s2加速前进,不能避免事故.
点评 本题是追击问题,要注意当两车速度相等时不会相撞,以后就不会相撞了,根据位移和时间关系再进行求解即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
 如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )
如图所示,在光滑小滑轮C正下方相距h的A处固定一电量为Q的点电荷,电量为q的带电小球B,用绝缘细线拴着,细线跨过定滑轮,另一端用适当大小的力拉住,使小球处于静止状态,这时小球与A点的距离为R,细线CB与AB垂直.(静电力恒量为k,环境可视为真空),若小球所受的重力的为 G,缓慢拉动细线(始终保持小球平衡)直到小球刚到滑轮的正下方过程中,拉力所做的功为W1,电场力做功为W2,则下列关系式正确的是( )| A. | W1=$\frac{mg}{2h}$(h2-R2) | B. | W2=GR(1-$\frac{R}{h}$) | C. | W1=$\frac{hkQq}{{R}^{2}}$(1-$\frac{R}{h}$) | D. | G=$\frac{khQq}{{R}^{3}}$ |
2.电荷+Q激发的电场中有A、B两点.质量为m,电量为q的带正电的粒子,自A点由静止释放后的运动中经过B点时的速度为v0,如果此粒子的质量为2q,质量为4m,仍从A点由静止释放(粒子重力均不计),则后一个粒子经过B点时的速度应为( )
| A. | 2v0 | B. | 4v0 | C. | $\frac{{v}_{0}}{2}$ | D. | $\frac{\sqrt{2}}{2}$v0 |
17.汽车以30m/s的速度做匀速直线运动,刹车的加速度大小为10m/s2,那么开始刹车后2s内与开始刹车后4s内汽车通过的位移之比为( )
| A. | 2:3 | B. | 8:9 | C. | 1:2 | D. | 1:1 |
 为了测定光在透明有机玻璃中的传播速度,实验室提供的器材有:矩形有机玻璃砖、木板、刻度尺、三角板、白纸、大头针.已知真空中的光速C.
为了测定光在透明有机玻璃中的传播速度,实验室提供的器材有:矩形有机玻璃砖、木板、刻度尺、三角板、白纸、大头针.已知真空中的光速C.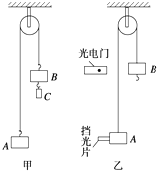 如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.
如图甲所示的装置叫做阿特伍德机,是英国数学家和物理学家阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律.某同学对该装置加以改进后用来验证机械能守恒定律,如图乙所示.