题目内容
2.电荷+Q激发的电场中有A、B两点.质量为m,电量为q的带正电的粒子,自A点由静止释放后的运动中经过B点时的速度为v0,如果此粒子的质量为2q,质量为4m,仍从A点由静止释放(粒子重力均不计),则后一个粒子经过B点时的速度应为( )| A. | 2v0 | B. | 4v0 | C. | $\frac{{v}_{0}}{2}$ | D. | $\frac{\sqrt{2}}{2}$v0 |
分析 粒子分别从A点由静止释放到达B点时,电场力做正功,根据动能定理研究它们的速度之比,从而得解.
解答 解:设A、B间的电势差为U,根据动能定理得:
对于任意一个粒子有:qU=$\frac{1}{2}m{v}^{2}$
可得:v=$\sqrt{\frac{2qU}{m}}$,U一定,则v与$\sqrt{\frac{q}{m}}$成正比,已知它们的电量之比1:2,质量之比1:4,则比荷$\frac{q}{m}$之比为2:1,所以速度之比为 v1:v2=$\sqrt{2}$:1.
因此 v2=$\frac{\sqrt{2}}{2}$v1=$\frac{\sqrt{2}}{2}$v0.
故选:D
点评 带电粒子在电场中运动要研究速度的关系,可以从能量的角度,根据动能定理进行研究.解答时要抓住AB间的电势差由电场决定,与所移动的电荷无关.

练习册系列答案
相关题目
13. 如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q方向可视运动.则在物块从可视运动到停止下的整个过程中( )
如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q方向可视运动.则在物块从可视运动到停止下的整个过程中( )
 如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q方向可视运动.则在物块从可视运动到停止下的整个过程中( )
如图所示,在足够大的粗糙水平绝缘面上固定着一个点电荷Q,将一个质量为m的带电物块q(可视为质点)在水平面上由静止释放,物块将在水平面上沿远离Q方向可视运动.则在物块从可视运动到停止下的整个过程中( )| A. | 物块的加速度一直变大 | |
| B. | 物块的加速度一直减小 | |
| C. | 电场力对物块做功的数值等于物块增加的机械能 | |
| D. | 电场对物块做功的数值等于系统摩擦产生的热 |

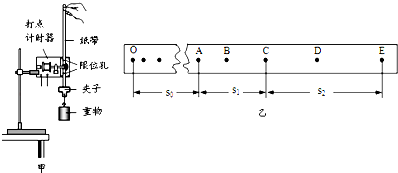
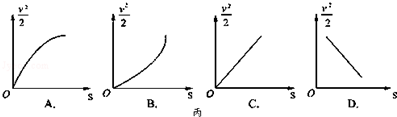
 在用打点计时器验证机械能守恒定律的实验中,质量m=1.00㎏的重物自由下落,打点计时器在纸带上打出一系列点.如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么:
在用打点计时器验证机械能守恒定律的实验中,质量m=1.00㎏的重物自由下落,打点计时器在纸带上打出一系列点.如图所示为选取的一条符合实验要求的纸带,O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2.那么: (1)图(b)为实验中所用打点计时器的学生电源.由学生电源可以判断该同学选用的是图(c)中的乙(填“甲”或“乙”)打点计时器.上述图(b)的安装中存在的错误有:①接线柱应接在交流电上
(1)图(b)为实验中所用打点计时器的学生电源.由学生电源可以判断该同学选用的是图(c)中的乙(填“甲”或“乙”)打点计时器.上述图(b)的安装中存在的错误有:①接线柱应接在交流电上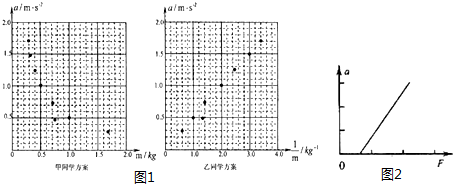
 有一条横截面积S=1mm2的铜导线,通过的电流I=1A,已知铜的密度ρ=8.9×103kg/m3,铜的摩尔质量M=6.4×10-2kg/mol,阿伏常量NA=6.62×1023mol-1,电子的电量e=-1.6×10-19C,求铜导线中自由电子定向移动的速率.(铜可视为一价元素)
有一条横截面积S=1mm2的铜导线,通过的电流I=1A,已知铜的密度ρ=8.9×103kg/m3,铜的摩尔质量M=6.4×10-2kg/mol,阿伏常量NA=6.62×1023mol-1,电子的电量e=-1.6×10-19C,求铜导线中自由电子定向移动的速率.(铜可视为一价元素)