题目内容
 如图所示,oa、ob、oc是竖直面内三根固定的光滑细杆,O、a、b、c、d位于同一圆周上,d点为圆周的最高点,c点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环都从o点无初速释放,用t1、t2、t3依次表示滑环到达a、b、c所用的时间,则
如图所示,oa、ob、oc是竖直面内三根固定的光滑细杆,O、a、b、c、d位于同一圆周上,d点为圆周的最高点,c点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环都从o点无初速释放,用t1、t2、t3依次表示滑环到达a、b、c所用的时间,则
- A.t1=t2=t3
- B.t3>t1>t2
- C.t1<t2<t3
- D.t1>t2>t3
D
分析:根据“等时圆”的适用条件构造出“等时圆”,作出图象,根据位移之间的关系即可判断运动时间.
解答: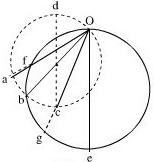 解:以O点为最高点,取合适的竖直直径oe作等时圆,交ob于b,如图所示,显然o到f、b、g、e才是等时的,比较图示位移oa>of,oc<og,故推得t1>t2>t3,
解:以O点为最高点,取合适的竖直直径oe作等时圆,交ob于b,如图所示,显然o到f、b、g、e才是等时的,比较图示位移oa>of,oc<og,故推得t1>t2>t3,
选项ABC错误,D正确.
故选D
点评:如果不假思考,套用结论,就会落入等时圆”的陷阱,要注意o点不是最高点,难度适中.
分析:根据“等时圆”的适用条件构造出“等时圆”,作出图象,根据位移之间的关系即可判断运动时间.
解答:
 解:以O点为最高点,取合适的竖直直径oe作等时圆,交ob于b,如图所示,显然o到f、b、g、e才是等时的,比较图示位移oa>of,oc<og,故推得t1>t2>t3,
解:以O点为最高点,取合适的竖直直径oe作等时圆,交ob于b,如图所示,显然o到f、b、g、e才是等时的,比较图示位移oa>of,oc<og,故推得t1>t2>t3,选项ABC错误,D正确.
故选D
点评:如果不假思考,套用结论,就会落入等时圆”的陷阱,要注意o点不是最高点,难度适中.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 两物体M、m用跨过光滑定滑轮的轻绳相连,如图所示,OA、OB与水平面的夹角分别为30°、60°,M、m均处于静止状态.则( )
两物体M、m用跨过光滑定滑轮的轻绳相连,如图所示,OA、OB与水平面的夹角分别为30°、60°,M、m均处于静止状态.则( )| A、绳OA的拉力大于绳OB的拉力 | B、绳OA的拉力小于绳OB的拉力 | C、m受到水平面的静摩擦力的方向水平向左 | D、m受到水平面的静摩擦力的方向水平向右 |
 如图所示,OA、OB、OC三段轻绳结于O点,下方轻绳OC悬挂质量为m1=0.3kg的物体甲.轻绳OB水平,B端与放置在水平面上的质量为m2=2kg的物体乙相连,物体乙恰好处于静止状态,已知物体乙与地面间的动摩擦因数为μ=0.2,重力加速度g取10m/s2,可认为最大静摩擦力与滑动摩擦力相等.求:
如图所示,OA、OB、OC三段轻绳结于O点,下方轻绳OC悬挂质量为m1=0.3kg的物体甲.轻绳OB水平,B端与放置在水平面上的质量为m2=2kg的物体乙相连,物体乙恰好处于静止状态,已知物体乙与地面间的动摩擦因数为μ=0.2,重力加速度g取10m/s2,可认为最大静摩擦力与滑动摩擦力相等.求: 如图所示,oa、ob、oc是竖直面内三根固定的光滑细杆,O、a、b、c、d位于同一圆周上,d点为圆周的最高点,c点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环都从o点无初速释放,用t1、t2、t3依次表示滑环到达a、b、c所用的时间,则( )
如图所示,oa、ob、oc是竖直面内三根固定的光滑细杆,O、a、b、c、d位于同一圆周上,d点为圆周的最高点,c点为最低点.每根杆上都套着一个小滑环(图中未画出),三个滑环都从o点无初速释放,用t1、t2、t3依次表示滑环到达a、b、c所用的时间,则( ) 如图所示,OA、OB两根绳子系着一个质量为m=0.5Kg的小球,两绳的A、B端分别固定在竖直转动轴上,OA绳长L=2m,两绳都拉直时与轴的夹角分别为370和530,(sin37°=0.6 cos37°=0.8 g=10m/s2) 求:
如图所示,OA、OB两根绳子系着一个质量为m=0.5Kg的小球,两绳的A、B端分别固定在竖直转动轴上,OA绳长L=2m,两绳都拉直时与轴的夹角分别为370和530,(sin37°=0.6 cos37°=0.8 g=10m/s2) 求: (2012?上海模拟)如图所示,OA、OB是竖直面内两根固定的光滑细杆,O、A、B、C位于同一圆周上,C点为圆周的最高点,B点为最低点.每根杆上都套着一个小滑环(图中未画出),两个滑环都从O点无初速释放,用t1、t2分别表示滑环到达A、B所用的时间,则( )
(2012?上海模拟)如图所示,OA、OB是竖直面内两根固定的光滑细杆,O、A、B、C位于同一圆周上,C点为圆周的最高点,B点为最低点.每根杆上都套着一个小滑环(图中未画出),两个滑环都从O点无初速释放,用t1、t2分别表示滑环到达A、B所用的时间,则( )