题目内容

（2012?上海模拟）如图所示，OA、OB是竖直面内两根固定的光滑细杆，O、A、B、C位于同一圆周上，C点为圆周的最高点，B点为最低点．每根杆上都套着一个小滑环（图中未画出），两个滑环都从O点无初速释放，用t1、t2分别表示滑环到达A、B所用的时间，则（　　）
分析：根据“等时圆”的适用条件构造出“等时圆”，作出图象，根据位移之间的关系即可判断运动时间．
解答：解：以O点为最高点，取合适的竖直直径OF作等时圆，可知从O点运动到A点和运动到D点的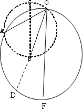时间相等，所以无初速从O点运动到B点的时间小于运动到D点的时间，故t1＞t2．故C正确，A、B、D错误．
故选C．
点评：如果不加思考，套用结论，就会落入等时圆”的陷阱，要注意o点不是最高点，难度适中．
练习册系列答案
相关题目
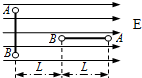（2012?上海模拟）如图所示，绝缘杆两端固定带电小球A和B，轻杆处于水平向右的匀强电场中，不考虑两球之间的相互作用．初始时杆与电场线垂直，将杆右移的同时顺时针转过90°，发现A、B两球电势能之和不变．根据如图给出的位置关系，下列说法正确的是（　　）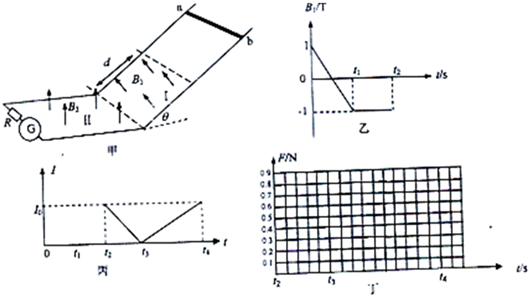
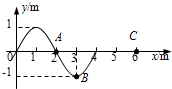（2012?上海模拟）如图（甲）所示，两个水平和倾斜光滑直导轨都通过光滑圆弧对接而成，相互平行放置，两导轨相距L=lm，倾斜导轨与水平面成θ=300角，倾斜导轨的下面部分处在一垂直斜面的匀强磁场区I中，I区中磁场的磁感应强度B1随时间变化的规律如图（乙）所示垂直斜面向上为正值，图中t1、t2未知．水平导轨足够长，其左端接有理想灵敏电流计G（内阻不计）和定值电阻R=3Ω，水平导轨处在一竖直向上的匀强磁场区Ⅱ中，Ⅱ区中的磁场恒定不变，磁感应强度大小为B2=1T，在t=0时刻，从斜轨上磁场I区外某处垂直于导轨水平静止释放一金属棒ab，棒的质量m=0．l kg，棒的电阻r=2Ω，棒下滑时与导轨保持良好接触，设棒通过光滑圆弧前后速度大小不变，导轨的电阻不计．若棒在斜面上向下滑动的整个过程中，灵敏电流计指针稳定时显示的电流大小相等，t2时刻进入水平轨道，立刻对棒施一平行于框架平面沿水平且与杆垂直的外力．（g取10m/s2）求：
（1）ab棒进入磁场区I时速度V的大小；（2）磁场区I在沿斜轨方向上的宽度d；
（3）棒从开始运动到刚好进入水平轨道这段时间内ab棒上产生的热量Q；
（4）若棒在t2时刻进入水平导轨后，电流计G的电流I随时间t变化的关系如图（丙）所示（而未知），已知t2到t3的时间为0.5s，t3到t4的时间为1s，请在图（丁）中作出t2到t4时间内外力大小F随时间t变化的函数图象．（从上向下看逆时针方向为电流正方向）
（2012?上海模拟）关于波的干涉和衍射现象，下列说法中正确的是（　　）
（2012?上海模拟）一列沿x正方向传播的简谐波t=0时刻的波形如图所示，t=0.2s时C点开始振动，则（　　）
（2012?上海模拟）在一次国际城市运动会中，要求运动员从高为H=4m的平台上A点由静止出发，沿着动摩擦因数为μ=0.2的滑道向下运动到B点后水平滑出，最后落在水池中．滑道的水平距离L大小不变，设滑道的水平距离为L=5m，B点的高度h可由运动员自由调节，A点不动，AB长度可以调整．（取g=10m/s2） 求：
（1）运动员要达到最大水平运动距离，B点的高度h应调为多大？平抛过程的最大水平距离Smax为多少？
（2）为了研究物体从B点沿光滑抛物线轨道顶端无初速下滑的运动，制做一个与第（1）中运动员平抛轨迹完全相同的光滑轨道，并将该轨道固定在与BC曲线重合的位置，让另一物体P沿该轨道无初速下滑（下滑过程中始终不会脱离轨道），则物体P通过轨道最低点C时的水平分速度和竖直分速度大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网